Bonjour j'ai cet exercice a résoudre. Je bute sur le début de la partie 2.
dans tout l'exercice E désigne et K espace vectoriel de dimension 3 et de base B=(e1,e2,e3)
soit f lendormophisme de E defini par :
f(e1)=e1+3e2+3e3
f(e2)=-3e1-5e2-3e3
f(e3)=3e1+3e2+e3
On convient de noter que
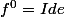
et
)
On note (;)n)nEN et (;)n)nEN les suites définies par

o=0 ,

o=1
et

n E N

n+1=-;)n+;)n

n+1=2;)n
-Montrer que

n E N
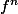
=

nf+;)nIde
-Montrer que la suite (Un)=;)n +

n est constante et montrer que la suite (Vn)=-2;)n +

n est gémotrique. Déterminer le terme général Un en fonction de n ainsi que le terme Vn. En déduire les expressions

n et de

n en fonction de n et exprimer f^n comme combinaison linéaire de f et de Ide.
Si qq a une piste ...
