Formes quadratiques définies positives.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 03 Fév 2013, 13:27
Bonjour à tous,
J'ai une question de méthode. L'exercice est tout ce qu'il y a de plus banal et de plus typique, mais je ne sais quelle méthode adopter.
Dire si ces deux formes quadratiques sur
sont définies positives.
 \, = \, x_1^2 \, + \, 2 \, x_2^2 \, + \, 3 \, x_1 \, x_2)
 \, = \, 2 \, x_1^2 \, + \, 3 \, x_2^2 \, + \, 4 \, x_1 \, x_2)
Q est définie positive si et seulement si
 \, \Rightarrow \, Q(x) > 0)
si et seulement si
 \geq 0 \\ Q(x)=0 \, \Rightarrow \, x \, = \,(0,0) \end{cases})
Je vous remercie,
Deluxor
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 03 Fév 2013, 13:40
Hello !
T'as essayé quelques valeurs de x pour Q_1 ?
Genre x = (1,-1) ?
Pour Q_2, faudrait penser à écrire la forme quadratique comme somme de deux carrés.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 03 Fév 2013, 13:51
Salut
Joker62,
Comme
 = 0)
, alors
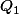
n'est pas définie positive. Ca suffit comme justification, non?
Pour
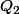
, est-ce juste?
La matrice de sa forme bilinéaire symétrique associée est :
)
)
On cherche les valeurs propres
:
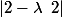
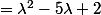
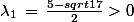
et
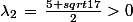
Donc
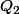
est définie positive.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
par wserdx » 03 Fév 2013, 14:01
Comme ces cas ne sont pas trop compliqués, on peut aussi rechercher les sommes (ou différences) de carrés:
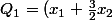^2 - \frac{1}{4} x_2^2)
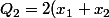^2 + x_2^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
