Partition d'un groupe (×) non commutatif
19 messages
- Page 1 sur 1
partition d'un groupe (×) non commutatif
Bonjour à toutes et à tous
L'ensemble GLr(Z/pZ) est l'ensemble des matrices carrées r×r inversibles
à coefficients dans Z/pZ ( p premier)
(GLr(Z/pZ),×) est un groupe non commutatif
U est l'ensemble généré par un élément m de GLr(Z/pZ)
(U,×) est un groupe abélien
La partition GLr(Z/pZ)/U peut-elle avoir moins de classes (U + les classes latérales à gauche) qu'il y a d'éléments dans U
Sur des exemples j'ai constaté que non mais je n'arrive pas à savoir si c'est toujours vrai
Par avance merci pour l'aide
@+
damville
L'ensemble GLr(Z/pZ) est l'ensemble des matrices carrées r×r inversibles
à coefficients dans Z/pZ ( p premier)
(GLr(Z/pZ),×) est un groupe non commutatif
U est l'ensemble généré par un élément m de GLr(Z/pZ)
(U,×) est un groupe abélien
La partition GLr(Z/pZ)/U peut-elle avoir moins de classes (U + les classes latérales à gauche) qu'il y a d'éléments dans U
Sur des exemples j'ai constaté que non mais je n'arrive pas à savoir si c'est toujours vrai
Par avance merci pour l'aide
@+
damville
utilisation de l'ordre de GLr(Fp)
Merci Doraki
C'est vrai que j'avais oublié de préciser que n était un entier naturel strictement supérieur à 1
|=p^{\frac{r(r-1)}{2}}(p^r-1)(p^{r-1}-1)\ldots(p^2-1)(p-1))
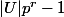
C'est vrai que j'avais oublié de préciser que n était un entier naturel strictement supérieur à 1
damville a écrit:Merci Doraki
C'est vrai que j'avais oublié de préciser que n était un entier naturel strictement supérieur à 1
bonjour , pour |U| ça va, je comprends le truc en considérant le polynôme caractéristique, les puissances de U s'expriment comme des polynômes en U de degré r-1 donc au max on en trouve p^r différents. Par contre pour |Gl_r(Fp)|??? une indication pour un curieux, merci.
(on a grossièrement |Gl_r(Fp)|<p^r² mais je ne comprends pas du tout l'égalité )
Compte le nombre de familles libres de 1 vecteur de Fp^r
Ensuite compte le nombre de manière d'ajouter un 2ème vecteur à chaque famille libre de 1 vecteur pour avoir une famille libre de 2 vecteurs.
Ensuite compte le nombre de manière d'ajouter un 3ème vecteur à chaque famille libre de 2 vecteurs pour avoir une famille libre de 3 vecteurs.
etc.
Ensuite compte le nombre de manière d'ajouter un 2ème vecteur à chaque famille libre de 1 vecteur pour avoir une famille libre de 2 vecteurs.
Ensuite compte le nombre de manière d'ajouter un 3ème vecteur à chaque famille libre de 2 vecteurs pour avoir une famille libre de 3 vecteurs.
etc.
Doraki a écrit:Compte le nombre de familles libres de 1 vecteur de Fp^r
Ensuite compte le nombre de manière d'ajouter un 2ème vecteur à chaque famille libre de 1 vecteur pour avoir une famille libre de 2 vecteurs.
Ensuite compte le nombre de manière d'ajouter un 3ème vecteur à chaque famille libre de 2 vecteurs pour avoir une famille libre de 3 vecteurs.
etc.
merci beaucoup, je vais réfléchir à cela à partir de cette piste.
Bonjour Doraki et jlb
Comment feriez-vous pour expliquer:
"pour |U| ça va, je comprends le truc en considérant le polynôme caractéristique, les puissances de U s'expriment comme des polynômes en U de degré r-1 donc au max on en trouve p^r différents"
... à quelqu'un qui fait très difficilement la liaison entre les matrices et les polynômes irréductibles ?
Par avance merci
damville
Comment feriez-vous pour expliquer:
"pour |U| ça va, je comprends le truc en considérant le polynôme caractéristique, les puissances de U s'expriment comme des polynômes en U de degré r-1 donc au max on en trouve p^r différents"
... à quelqu'un qui fait très difficilement la liaison entre les matrices et les polynômes irréductibles ?
Par avance merci
damville
damville a écrit:Bonjour Doraki et jlb
Comment feriez-vous pour expliquer:
"pour |U| ça va, je comprends le truc en considérant le polynôme caractéristique, les puissances de U s'expriment comme des polynômes en U de degré r-1 donc au max on en trouve p^r différents"
... à quelqu'un qui fait très difficilement la liaison entre les matrices et les polynômes irréductibles ?
Par avance merci
damville
à vérifier: m annule son polynôme caractéristique ( th de Cayley, joli preuve à partir de matrice compagnon), c'est un polynôme de degré r , tu as donc une relation de la forme 0 =(-1)^r m^r + a(r-1)m^(r-1) + ....+ a(0)Id , tu peux donc exprimer les puissances de m à partir de Id, m, m²,...m^r-1. ( le 0 est à interpréter comme l'endomorphisme nul!!): il suffit ensuite de compter le nombre d'écriture possible à partir de I,m²....,m^r-1 pour obtenir une majoration de ||
valeur maximale de K tel que [m]^K=[I]
Bonjour à toutes et à tous
On considère l'action du groupe (GLr( /n
/n ),multiplication des matrices) dans l'ensemble des permutations de
),multiplication des matrices) dans l'ensemble des permutations de ^r)
A une matrice choisie [m] correspond une permutation dans laquelle les éléments de^r) sont groupés par orbites (voir Jean-Pierre Serre)
sont groupés par orbites (voir Jean-Pierre Serre)
(0,0,...,0) appartient toujours à l'orbite de "longueur" 1 qui est ((0,0,...,0))
L'orbite la plus longue possible si elle existe comportera tous les autres éléments de^r)
Cette orbite est:
([m](u1,u2,...,ur), [m]^2((u1,u2,...,ur), [m]^3(u1,u2,...,ur),........, [m]^K(u1,u2,...,ur))
avec [m]^K(u1,u2,...,ur)=(u1,u2,...,ur)
L'ordre de^r) est égal à
est égal à 
donc l'orbite la plus longue possible aura une longueur égale à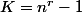
ma question : est-ce que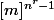 est forcément égal à [I] ?
est forcément égal à [I] ?
Merci et bonne journée
On considère l'action du groupe (GLr(
A une matrice choisie [m] correspond une permutation dans laquelle les éléments de
(0,0,...,0) appartient toujours à l'orbite de "longueur" 1 qui est ((0,0,...,0))
L'orbite la plus longue possible si elle existe comportera tous les autres éléments de
Cette orbite est:
([m](u1,u2,...,ur), [m]^2((u1,u2,...,ur), [m]^3(u1,u2,...,ur),........, [m]^K(u1,u2,...,ur))
avec [m]^K(u1,u2,...,ur)=(u1,u2,...,ur)
L'ordre de
donc l'orbite la plus longue possible aura une longueur égale à
ma question : est-ce que
Merci et bonne journée
Salut,
J'ai un peu du mal à comprendre ton arguments concernant la longueur des orbites : l'ordre d'une permutation est en générale plus grand que la plus grande des orbites.
Par exemple sur l'ensemble E={1,2,...,7} la permutation (écrite sous forme de cycles disjoints)
p = (1 2 3) (4 5 6 7)
scinde l'ensemble E en deux orbites de taille respective 3 et 4 et en fait l'ordre est ppcm(4,3)=12.
Sinon, concernant l'ordre maxi d'une matrice, l'argument de doraki me semble très simple :
F=vect{Id,U,U^2,...U^(r-1)} est non seulement un espace vectoriel, mais c'est aussi un anneau (Cayley Hamilton) donc toutes les puissances de U sont dans F qui est de cardinal p^r.
Conclusion : il y a moins de p^r puissances de U différentes.
Attention, au fait que, vu que F n'est pas un groupe on ne peut pas conclure que l'ordre du U divise p^r. Pour pouvoir utiliser un tel argument, il faudrait avoir le cardinal de l'ensemble des éléments inversibles de F qui est clairement un groupe (mais je ne sais pas si c'est facile...)
J'ai un peu du mal à comprendre ton arguments concernant la longueur des orbites : l'ordre d'une permutation est en générale plus grand que la plus grande des orbites.
Par exemple sur l'ensemble E={1,2,...,7} la permutation (écrite sous forme de cycles disjoints)
p = (1 2 3) (4 5 6 7)
scinde l'ensemble E en deux orbites de taille respective 3 et 4 et en fait l'ordre est ppcm(4,3)=12.
Sinon, concernant l'ordre maxi d'une matrice, l'argument de doraki me semble très simple :
F=vect{Id,U,U^2,...U^(r-1)} est non seulement un espace vectoriel, mais c'est aussi un anneau (Cayley Hamilton) donc toutes les puissances de U sont dans F qui est de cardinal p^r.
Conclusion : il y a moins de p^r puissances de U différentes.
Attention, au fait que, vu que F n'est pas un groupe on ne peut pas conclure que l'ordre du U divise p^r. Pour pouvoir utiliser un tel argument, il faudrait avoir le cardinal de l'ensemble des éléments inversibles de F qui est clairement un groupe (mais je ne sais pas si c'est facile...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour à toutes et à tous
Merci Ben
J'ai dû choisir le mauvais mot (permutation) c'était peut-être bijection qu'il fallait utiliser
Quand tu multiplies par la matrice (choisie une fois pour toute) un r-uplet , tu en obtiens un autre et un seul (son image)
Si tu mets en relation chacun des r-uplets de
r-uplets de ^{r}) avec son image le nombre de couples (r-uplet,image de ce r-uplet) est au maximum égal à
avec son image le nombre de couples (r-uplet,image de ce r-uplet) est au maximum égal à 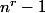 , dans la même orbite ((r-uplet N°1,r-uplet N°2,r-uplet N°3,....,r-uplet N°K)) avec r-uplet N°i+1 image du r-uplet N°i et r-uplet N°1 image du r-uplet N°K mais n'est effectivement égal à ce maximum que pour certaines matrices choisies
, dans la même orbite ((r-uplet N°1,r-uplet N°2,r-uplet N°3,....,r-uplet N°K)) avec r-uplet N°i+1 image du r-uplet N°i et r-uplet N°1 image du r-uplet N°K mais n'est effectivement égal à ce maximum que pour certaines matrices choisies
par exemple pour la matrice de)
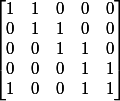 c'est effectivement le cas
c'est effectivement le cas
il y a une orbite de longueur 1 qui est ((0,0,0,0,0)) et 1 orbite de longueur 31 qui est
((0,0,0,0,1),(0,0,0,1,1),(0,0,0,1,0,0),.....,(0,1,0,1,0,1),(1,1,1,1,1))
mais pour la matrice de)
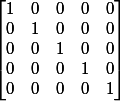 ce n'est pas le cas la longueur maximale d'une orbite est 1
ce n'est pas le cas la longueur maximale d'une orbite est 1
et il y 32 orbites de longueur 1 qui sont: orbite N°1 ((0,0,0,0,0)) orbite N°2 ((0,0,0,0,1)) ... etc ... orbite N°32 ((1,1,1,1,1))
Bonne journée et encore merci (je réfléchis sur la fin de ton message à partir de "sinon")
Merci Ben
J'ai dû choisir le mauvais mot (permutation) c'était peut-être bijection qu'il fallait utiliser
Quand tu multiplies par la matrice (choisie une fois pour toute) un r-uplet , tu en obtiens un autre et un seul (son image)
Si tu mets en relation chacun des
par exemple pour la matrice de
il y a une orbite de longueur 1 qui est ((0,0,0,0,0)) et 1 orbite de longueur 31 qui est
((0,0,0,0,1),(0,0,0,1,1),(0,0,0,1,0,0),.....,(0,1,0,1,0,1),(1,1,1,1,1))
mais pour la matrice de
et il y 32 orbites de longueur 1 qui sont: orbite N°1 ((0,0,0,0,0)) orbite N°2 ((0,0,0,0,1)) ... etc ... orbite N°32 ((1,1,1,1,1))
Bonne journée et encore merci (je réfléchis sur la fin de ton message à partir de "sinon")
Ben... si, il me semble que "permutation" c'est le bon mot : lorsque tu "fait agir un groupe sur un ensemble" comme là ou tu fait agir GLr(k) sur k^r, c'est la même chose que de se donner un morphisme de ton groupe dans l'ensemble des permutations de l'ensemble.
Donc je reprend ma question : comment montre tu que la longueur de la plus grande orbite soit forcément égale à l'ordre de U.
Ce n'est le cas que si le taille des cette "plus grande orbite" et un multiple de la taille de toutes les autres orbites.
C'est effectivement le cas sur les 2 exemples que tu propose. Mais quid du cas général ?
Exemple :)
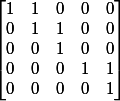
Edit (à midi donc plus réveillé que ce matin avant d'aller en cours...)
La matrice que j'avais mis n'était pas inversible.... je la modifie.
Donc je reprend ma question : comment montre tu que la longueur de la plus grande orbite soit forcément égale à l'ordre de U.
Ce n'est le cas que si le taille des cette "plus grande orbite" et un multiple de la taille de toutes les autres orbites.
C'est effectivement le cas sur les 2 exemples que tu propose. Mais quid du cas général ?
Exemple :
Edit (à midi donc plus réveillé que ce matin avant d'aller en cours...)
La matrice que j'avais mis n'était pas inversible.... je la modifie.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
essai de généralisation
Bonjour à toutes et à tous
C'était difficile à écrire j'espère que je ne me suis pas planté
) est un anneau commutatif fini d'ordre |k|
est un anneau commutatif fini d'ordre |k|
) est un groupe abélien
est un groupe abélien
) est un k-module sur
est un k-module sur 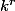
,\cdots,(a_{r1},a_{r2},\cdots,a_{rr})))
est une base de ce k-module
Tout élément) de
de 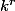 s'écrit de façon unique sous la forme de la combinaison linéaire suivante
s'écrit de façon unique sous la forme de la combinaison linéaire suivante
= \sum_{i=1}^r t_i\otimes(a_{i,1},a_{i,2},\cdots,a_{i,r}))
qui peut s'écrire sous forme matricielle
= \begin{bmatrix} a_{1,1} & \cdots & a_{1,1} \\ \cdots & \cdots & \cdots \\ a_{r,1} & \cdots & a_{r,r} \\ \end{bmatrix} . (t_1,t_2,\cdots,t_r) = <br />[m] . (t_1,t_2,\cdots,t_r))
On considère l'application
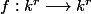
 \longrightarrow [m].(u_1,u_2,\cdots,u_r))
et on considère l'orbite des images des images des images ... de)
Cette orbite est
, [m]^2 (u_1,u_2,\cdots,u_r),......, [m]^q (u_1,u_2,\cdots,u_r), .....))
On note_q = [m]^q (u_1,u_2,\cdots,u_r))
On sait que [m].(0,0,...,0)=(0,0,...,0) et donc que (0,0,...,0) est dans une orbite de longueur 1
Il reste donc |k|^r éléments de k^r à placer dans des orbites. Quelle est alors la plus grande valeur que pourrait prendre q longueur de l'orbite dans laquelle se trouve) . C'est le nombre d'éléments de l'ensemble k^r\{(0,0,...,0)}
. C'est le nombre d'éléments de l'ensemble k^r\{(0,0,...,0)}
c'est à dire |k|^r - 1
C'est là que je repose ma question
Est-on certain que dans ce cas pour lequel on ne trouve qu' une orbite de longueur 1 et une orbite de longueur |k|^r-1
on est certain que [m]^(|k|^r-1)=[I]
Merci pour les corrections
Bonne journée à toutes et à tous
damville
C'était difficile à écrire j'espère que je ne me suis pas planté
est une base de ce k-module
Tout élément
qui peut s'écrire sous forme matricielle
On considère l'application
et on considère l'orbite des images des images des images ... de
Cette orbite est
On note
On sait que [m].(0,0,...,0)=(0,0,...,0) et donc que (0,0,...,0) est dans une orbite de longueur 1
Il reste donc |k|^r éléments de k^r à placer dans des orbites. Quelle est alors la plus grande valeur que pourrait prendre q longueur de l'orbite dans laquelle se trouve
c'est à dire |k|^r - 1
C'est là que je repose ma question
Est-on certain que dans ce cas pour lequel on ne trouve qu' une orbite de longueur 1 et une orbite de longueur |k|^r-1
on est certain que [m]^(|k|^r-1)=[I]
Merci pour les corrections
Bonne journée à toutes et à tous
damville
damville a écrit:C'est là que je repose ma question
Est-on certain que dans ce cas pour lequel on ne trouve qu' une orbite de longueur 1 et une orbite de longueur |k|^r-1
on est certain que [m]^(|k|^r-1)=[I]
J'ai pas bien compris la question...
Si c'est "dans le cas où il y a une orbite de longueur 1 et une de longueur |k|^r-1, peut on en déduire que l'ordre de m est |k|^r-1" alors la réponse est oui.
Dans le cas général, lorsque tu décompose une permutation en cycles disjoints (c'est ce que tu fait), l'ordre de la permutation, c'est le ppcm de l'ordre des cycles (= la taille des cycles)
Donc je le (re)dit, chercher la plus grande taille possible pour un cycle, dans l'absolu, ça donne pas vraiment d'infos sur l'ordre de la permutation.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Aprés, si tu veut vraiment écrire des trucs théoriques concernant l'ordre d'une matrice inversible (à coeff dans un corps K : je ne crois pas que ce soit valable dans un anneau), à mon avis, il faut essayer de trouve un groupe le plus petit possible contenant ta matrice pour pouvoir dire "l'ordre d'un élément divise l'ordre du groupe".
Or, si tu as le polynôme minimal P de ta matrice tu as un isomorphisme naturel de l'anneau K[X]/(P) dans le sous anneau de GLr(K) engendré par ta matrice m (qui envoie X sur m).
Donc l'ordre de m, c'est l'ordre de X dans K[X]/(P) et ça divise l'ordre du groupe (K[X]/(P))* des éléments inversibles de K[X]/(P) que l'on pourrait, par exemple, appeler) (indicatrice d'Euler).
(indicatrice d'Euler).
Par exemple, si P est irréductible, K[X]/(P) est un corps donc=card\big(K[X]/(P)\big)-1=|K|^{deg(P)}-1)
Si P n'est pas irréductible, je pense qu'on peut procéder comme pour l'indicatrice d'Euler "usuelle" sur Z pour calculer)
Or, si tu as le polynôme minimal P de ta matrice tu as un isomorphisme naturel de l'anneau K[X]/(P) dans le sous anneau de GLr(K) engendré par ta matrice m (qui envoie X sur m).
Donc l'ordre de m, c'est l'ordre de X dans K[X]/(P) et ça divise l'ordre du groupe (K[X]/(P))* des éléments inversibles de K[X]/(P) que l'on pourrait, par exemple, appeler
Par exemple, si P est irréductible, K[X]/(P) est un corps donc
Si P n'est pas irréductible, je pense qu'on peut procéder comme pour l'indicatrice d'Euler "usuelle" sur Z pour calculer
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Un ordre quand même bien limité
Salut
Merci Ben. Cela ne sert à rien de trouver la plus grande valeur possible de l'ordre alors surtout
que pour certaines matrices de GLr(Z/nZ) [m]^(n^r-1) n'est même pas égal à [I]
Par exemple la matrice [m] ci-dessous appartenant à GL9(Z/26Z) a sa puissance 26^9-1 non égale à [I]

On se demande quel est l'ordre K de cette matrice
K divise PGCM(|GL9(Z/2Z)|,|GL9(Z/13Z)|) =(2^8-1)...(2^2-1)(2^1-1), 13^{\frac{9 \times 8}{2}}(13^9-1)(13^8-1)...(13^2-1)(13^1-1))) =
=
PGCM(699612310033197642547200, 15554562965023219559268324311468001299370449452142
6138500554439860349627930191311709562470400)=
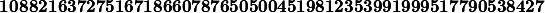
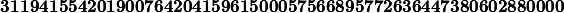
C'est quand même rassurant de savoir que l'ordre ne dépasse pas 26^9-1= 5429503678975 plutôt qu'uniquement savoir que c'est un diviseur d'un nombre à plus de 100 chiffres
Oui on est aidé par les facteurs premiers qui permettent d'obtenir l'ordre K= 45 658 261 185 et comme cet ordre n'est pas un diviseur de
26^9-1= 5 429 503 678 975 alors [m]^(26^9-1) n'est pas égal à [I]
Alors Ben comment fais-tu s'il te plait pour montrer que dans le cas des deux orbites seulement
une de longueur 1 l'autre de longueur |k|^r -1 on a toujours [m]^(|k|^r-1)=[I]
Bébête je ne trouve pas
Merci
@+ Damville
Merci Ben. Cela ne sert à rien de trouver la plus grande valeur possible de l'ordre alors surtout
que pour certaines matrices de GLr(Z/nZ) [m]^(n^r-1) n'est même pas égal à [I]
Par exemple la matrice [m] ci-dessous appartenant à GL9(Z/26Z) a sa puissance 26^9-1 non égale à [I]
On se demande quel est l'ordre K de cette matrice
K divise PGCM(|GL9(Z/2Z)|,|GL9(Z/13Z)|) =
PGCM(699612310033197642547200, 15554562965023219559268324311468001299370449452142
6138500554439860349627930191311709562470400)=
C'est quand même rassurant de savoir que l'ordre ne dépasse pas 26^9-1= 5429503678975 plutôt qu'uniquement savoir que c'est un diviseur d'un nombre à plus de 100 chiffres
Oui on est aidé par les facteurs premiers qui permettent d'obtenir l'ordre K= 45 658 261 185 et comme cet ordre n'est pas un diviseur de
26^9-1= 5 429 503 678 975 alors [m]^(26^9-1) n'est pas égal à [I]
Alors Ben comment fais-tu s'il te plait pour montrer que dans le cas des deux orbites seulement
une de longueur 1 l'autre de longueur |k|^r -1 on a toujours [m]^(|k|^r-1)=[I]
Bébête je ne trouve pas
Merci
@+ Damville
Si tu veut un exemple "plus petit" prend
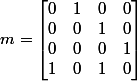 dans Z/2Z
dans Z/2Z
Comme c'est une "matrice compagnon", poly.min. = poly.char. et il se "lit" directement sur la ligne du bas de la matrice : c'est^2) et, modulo P on voit immédiatement que X est d'ordre 6 (donc m aussi). Or 6 ne divise pas |k|^r-1=2^4-1=15 (par contre il divise bien
et, modulo P on voit immédiatement que X est d'ordre 6 (donc m aussi). Or 6 ne divise pas |k|^r-1=2^4-1=15 (par contre il divise bien =2^4-2^2=12) )
)
De toute façon, là où ça me semble clair que ton truc est "foireux", c'est qu'une matrice de taille rxr, tu peut augmenter sa taille r en ajoutant des 1 sur la diagonale et que ça ne change clairement pas son ordre donc si son ordre devait forcément diviser |k|^r-1, il devrait aussi diviser tout les |k|^n-1 où n>=k et ça, c'est pas raisonnable...
Là, c'est un résultat très classique concernant les permutations : toute permutation (sur un ensemble fini évidement) se décompose en produit de cycles disjoints (qui commutent donc entre eux) et cette décomposition est unique à l'ordre des facteurs prés (tout ça n'est pas très dur à montrer vu que les supports des cycles, ce sont les différentes orbites)
Quand tu élève ta permutation à la puissance n, ça élève tout les cycles à la puissance n (car ils commutent) et le coté "unicité" de la décomposition te dit que ta permutation à la puissance n ne vaut Id que si chaque cycle à la puissance n vaut Id, donc si n est multiple de la longueur de tout les cycle. Le plus petit tel n est le ppcm des longueurs des cycles.
Comme c'est une "matrice compagnon", poly.min. = poly.char. et il se "lit" directement sur la ligne du bas de la matrice : c'est
De toute façon, là où ça me semble clair que ton truc est "foireux", c'est qu'une matrice de taille rxr, tu peut augmenter sa taille r en ajoutant des 1 sur la diagonale et que ça ne change clairement pas son ordre donc si son ordre devait forcément diviser |k|^r-1, il devrait aussi diviser tout les |k|^n-1 où n>=k et ça, c'est pas raisonnable...
Non seulement on a [m]^(|k|^r-1)=[I], mais en fait |k|^r-1 est exactement l'ordre de m (i.e. ça ne pas [I] pour des puissances plus petites)damville a écrit:Alors Ben comment fais-tu s'il te plait pour montrer que dans le cas des deux orbites seulement
une de longueur 1 l'autre de longueur |k|^r -1 on a toujours [m]^(|k|^r-1)=[I]
Là, c'est un résultat très classique concernant les permutations : toute permutation (sur un ensemble fini évidement) se décompose en produit de cycles disjoints (qui commutent donc entre eux) et cette décomposition est unique à l'ordre des facteurs prés (tout ça n'est pas très dur à montrer vu que les supports des cycles, ce sont les différentes orbites)
Quand tu élève ta permutation à la puissance n, ça élève tout les cycles à la puissance n (car ils commutent) et le coté "unicité" de la décomposition te dit que ta permutation à la puissance n ne vaut Id que si chaque cycle à la puissance n vaut Id, donc si n est multiple de la longueur de tout les cycle. Le plus petit tel n est le ppcm des longueurs des cycles.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
