Relation d'Euleur - Produit scalaire

[upium666]

Bonjour à tous et à toutes !

A,B,C trois points donnés
Démontrer que pour tout point M :



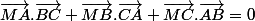
Jusques là pas de problème j'y suis arrivé (quoique ma méthode est un peu barbare : j'ai décomposé tous les vecteurs qui commencent par M en MA+le reste et ça m'a donné le résultat; ce serait gentil de me montrer s'il existe une méthode plus élégante)

Le problème se pose ici :

En déduire que les trois hauteurs d'un triangle sont concourantes

Comment puis-je faire ?

Merci ^^

[chan79]

Bonjour à tous et à toutes !

A,B,C trois points donnés
Démontrer que pour tout point M :



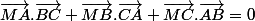
Jusques là pas de problème j'y suis arrivé (quoique ma méthode est un peu barbare : j'ai décomposé tous les vecteurs qui commencent par M en MA+le reste et ça m'a donné le résultat; ce serait gentil de me montrer s'il existe une méthode plus élégante)

Le problème se pose ici :

En déduire que les trois hauteurs d'un triangle sont concourantes

Comment puis-je faire ?

Merci ^^

bonjour
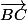
Tu peux remplacer par
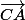
puis par etc je ne sais pas si c'est mieux

Pour la suite
Tu prends le point M, d'intersection de la hauteur issue de A et de la hauteur isuue de B
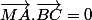
tu as donc et
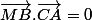
Ensuite tu utilises ta formule

[Zelda85]

Bonjour,

Comme tu as démontré l'égalité pour TOUT point M du plan, tu peux très bien dire qu'en réalité l'égalité est valable pour le point d'intersection de deux des hauteurs (Par exemple, si tu appelles ce point le point H, tu auras l'égalité vérifié pour ce point là).
Ainsi tu auras HA.BC + HB.CA + HC.AB = 0 (avec les fléches pour dire que ce sont des vecteurs).
HA.BC = 0 puisque (AH) est la hauteur issue de A dans le triangle ABC.
HB.CA =0 puisque (BH) est la hauteur issue de B dans le triangle ABC.
Donc on aura HC.AB = 0 (d'après la première égalité que tu as trouvé), ça veut dire que la droite (HC) est la troisième hauteur, DONC H appartient à cette hauteur, DONC H appartient aux trois hauteurs, donc les trois hauteurs d'un triangle sont concourantes !

Voilà,
En éspérant t'avoir aidé.

Zelda85

[upium666]

Pour la suite
Tu prends le point M, d'intersection de la hauteur issue de A et de la hauteur isuue de B
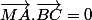
tu as donc et
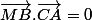
Ensuite tu utilises ta formule

D'accord mais en quoi ça montre que les hauteurs concourent en ce même point qui est M ?

[chan79]

D'accord mais en quoi ça montre que les hauteurs concourent en ce même point qui est M ?

=-(=0-(0+0)=0

donc (MC) perp à (AB)
les 3 hauteurs passent par M

[upium666]

Bonjour,

Comme tu as démontré l'égalité pour TOUT point M du plan, tu peux très bien dire qu'en réalité l'égalité est valable pour le point d'intersection de deux des hauteurs (Par exemple, si tu appelles ce point le point H, tu auras l'égalité vérifié pour ce point là).
Ainsi tu auras HA.BC + HB.CA + HC.AB = 0 (avec les fléches pour dire que ce sont des vecteurs).
HA.BC = 0 puisque (AH) est la hauteur issue de A dans le triangle ABC.
HB.CA =0 puisque (BH) est la hauteur issue de B dans le triangle ABC.
Donc on aura HC.AB = 0 (d'après la première égalité que tu as trouvé), ça veut dire que la droite (HC) est la troisième hauteur, DONC H appartient à cette hauteur, DONC H appartient aux trois hauteurs, donc les trois hauteurs d'un triangle sont concourantes !

Voilà,
En éspérant t'avoir aidé.

Zelda85

Merci c'est très clair mais j'ai toujours une question qui me dérange vraiment :/

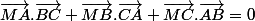
En quoi la relation implique-t-elle que M est l'intersection de 3 droites ?!

[chan79]

Merci c'est très clair mais j'ai toujours une question qui me dérange vraiment :/

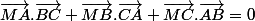
En quoi la relation implique-t-elle que M est l'intersection de 3 droites ?!

Cette formule est valable pour tout point M
Elle est valable si on met M à l'intersection de deux hauteurs

[upium666]

Cette formule est valable pour tout point M
Elle est valable si on met M à l'intersection de deux hauteurs

J'ai compris (j'espère !)

Si j'ai bien assimilé :

En posant : H l'intersection de deux hauteurs => La troisième droite est une hauteur et comme H rentre dans l'expression du produit scalaire imposé alors les 3 hauteurs sont concourantes

Est-ce bien cela ?

[chan79]

J'ai compris (j'espère !)

Si j'ai bien assimilé :

En posant : H l'intersection de deux hauteurs => La troisième droite est une hauteur et comme H rentre dans l'expression du produit scalaire imposé alors les 3 hauteurs sont concourantes

Est-ce bien cela ?

deux produits scalaires étant nuls, le troisième aussi puisque la somme des trois est nulle
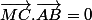
si par exemple, on arrive à , cela veut dire (MC) est la troisième hauteur. Donc ces 3 hauteurs passent par M ( appelé orthocentre)

[upium666]

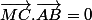
=> (MC) est la troisième hauteur

L'information qui me manquait était :

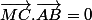
=> MC est perpendiculaire à AB => MC est une droite issue de C et perpendiculaire à AB => (MC) est la troisième hauteur

Je l'avais compris mais je suis, de nature, perturbé lorsqu'une étape manque :p

Merci à tous !

Problème résolu