Je cherche désespéremment à montrer que la conjecture suivante est fausse:
"si Up est un multiple de p alors p est premier".
la suite U est définie de la manière suivante: U(n+3) = U(n+1) + U(n) avec U(0) = 3, U(1) = 0 et U(2) =2
( j'ai testé la conjecture pour les 100 000 premiers entiers à l'aide d'Xcas ( à vrai est-ce que cela a du sens?, la réciproque est par contre vraie, ce n'est pas trop difficile à montrer)
Je vous remercie, si quelqu'un peut m'apporter de l'aide ou m'indiquer une référence car cela ne doit pas être facile.
A propos d'une suite "détectrice de nbs premiers"
7 messages
- Page 1 sur 1
patrickjaud a écrit:Bonjour,
j'ai simplement modélisé sous excel et il est vrai que pour les premiers termes cela marche ...
mais pour n= 125 on trouve : U(125)= 1842586692361260 = 125 * 14740693538890 (éviter de faire à la calculette ou à la main ....... , mais plutôt à faire au tableur)
En espérant t'avoir aidé !!!
Patrick Jaud, professeur indépendant en maths physique et chimie dans l'Eure Et loir, Le loiret (Chartres, Châteaudun, Orléans)
merci mais le calcul doit dépasser les capacités d'excel, pour ma part je trouve 1842586692361255!!
Incroyable ta suite.
c'est une suite polynomiale de la forme=a^n+(b+ic)^n+(b-ic)^n)
où a, b+ic et b-ic sont les racines de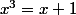
En effet je trouve que ta conjecture est fausse pour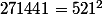 .
.
Y aurait-il un lien avec le test de lucas-lehmer?
c'est une suite polynomiale de la forme
où a, b+ic et b-ic sont les racines de
En effet je trouve que ta conjecture est fausse pour
- Code: Tout sélectionner
q:=true;
p:=[3,0,2];
t:=0;
for n:=3 to 1000000 do
p:= p[2..3] cat [p[1]+p[2]];
t:=n;
q:= q and (not IsDivisibleBy(p[3],n) or IsPrime(n));
if not q then break; end if;
end for;
t;
q;
Y aurait-il un lien avec le test de lucas-lehmer?
wserdx a écrit:Incroyable ta suite.
c'est une suite polynomiale de la forme
où a, b+ic et b-ic sont les racines de
En effet je trouve que ta conjecture est fausse pour 271441.
- Code: Tout sélectionner
q:=true;
p:=[3,0,2];
t:=0;
for n:=3 to 1000000 do
p:= p[2..3] cat [p[1]+p[2]];
t:=n;
q:= q and (not IsDivisibleBy(p[3],n) or IsPrime(n));
if not q then break; end if;
end for;
t;
q;
Y aurait-il un lien avec le test le lucas-lehmer?
je ne suis pas très doué!! est-ce qu'on ne dépasse pas les capacités de calcul avec de tels entiers? je ne connais pas les tailles limites permises pour qu'il n'y ait pas d'erreurs d'arrondis ( tu as utilisé mapple)? Si on peut considérer le nombre que tu as obtenu comme exact j'ai mon contre exemple et je t'en remercie!! sinon, il faut se creuser la tête et je crois que cela dépasse mes compétences. merci encore, je m'étais arreté à 100 000 et je n'avais pas osé lancer mon programme pour des entiers supérieurs!! car j'avais passé déjà dix minutes pour obtenir le résultat.
En tout cas merci de l'intérêt que tu y as apporté et si tu peux me confirmer que les calculs sont licites, je t'en remercie.
ps: j'ai trouvé cette suite sur le site de l'irem de Lyon ( séance utilisation Xcas par MERCAT C.) pour ceux que cela intéresse.
merci. mon problème est résolu. et en fait, j'ai trouvé un article sur ce type de suite, c'est un cas particuliers de suite de Padovan et il y 4 contre-exemples entre 1 et 18 000 000!!! (à vérifier toutefois)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
