Matrice symetrique définie positive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 27 Jan 2013, 12:19
par Bourguignon » 27 Jan 2013, 12:19
Bonjour soit la matrice
A=
\begin{pmatrix}
2& -1 & 0 & 0 \\
-1 & 2 & -1 & 0\\
0 & -1 & 2 & -1\\
0 & 0 & -1 & 2
\end{matrix}
Je l'ai écrit ainsi car ici le Latex bug. Donc c'est
A=
2 & -1 & 0 & 0
-1 & 2 & -1 & 0
0 & -1 & 2 & -1
0 & 0 & -1 & 2
Il faut démontrer que A est symetrique définie positive en calculant
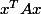
pour tout vecteur x de
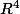
J'ai fait le calcul et je tombe sur x²+y²+z²+t²-xy-yz-zt . Ensuite je ne vois pas trop comment finir.
Merci
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 27 Jan 2013, 12:35
par adrien69 » 27 Jan 2013, 12:35
Yo,
Tu saurais factoriser un peu tout ça ? (réduction de Gauss)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Jan 2013, 13:22
par chan79 » 27 Jan 2013, 13:22
Bourguignon a écrit:Bonjour soit la matrice
A=
\begin{pmatrix}
2& -1 & 0 & 0 \\
-1 & 2 & -1 & 0\\
0 & -1 & 2 & -1\\
0 & 0 & -1 & 2
\end{matrix}
Je l'ai écrit ainsi car ici le Latex bug. Donc c'est
A=
2 & -1 & 0 & 0
-1 & 2 & -1 & 0
0 & -1 & 2 & -1
0 & 0 & -1 & 2
Il faut démontrer que A est symetrique définie positive en calculant
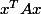
pour tout vecteur x de
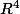
J'ai fait le calcul et je tombe sur x²+y²+z²+t²-xy-yz-zt . Ensuite je ne vois pas trop comment finir.
Merci
si on multiplie tout par 2
2x²+2y²+2z²+2t²
-2xy-2yz-2zt=2x²+2y²+2z²+2t²+
(x-y)²-x²-y²+
(y-z)²-y²-z²+
(z-t)²-z²-t²ensuite on simplifie
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 27 Jan 2013, 15:10
par Bourguignon » 27 Jan 2013, 15:10
avec 4 variables, je ne m'en souviens plus .
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 27 Jan 2013, 15:17
par Bourguignon » 27 Jan 2013, 15:17
Ok merci bien ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
