Bonjour,
Je suis étudiant en remise à niveau scientifique. J'ai l'exercice suivant à faire :
Trouver sur R la primitive de f qui vaut 0 en pi pour les fonctions f suivantes :
a. f(x) = sin x
b. f(x) = sin 2x
c. f(x) = sin x + cos x
d. f(x) = cos(nx) lorsque n est entier
e. f(x) = sin² x
Je ne comprends pas du tout comment faire. Si quelqu'un pouvait m'expliquer avec des cas concrets. Je suis précise que je suis titulaire à la base d'un bac STG.
Merci d'avance.
Primitive
3 messages
- Page 1 sur 1
Bonjour,
Pour : = \sin (x) $) .
.
Il existe une infinité de primitives de qu'on regroupe dans l'ensemble :
qu'on regroupe dans l'ensemble : 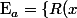 = \int_{a}^x \sin (x) dx + R(a ) \ \mid \ a \in \mathbb{R} \} $) .
.
Dans le cas de ton exercice, on cherche une seule primitive particulière qui appartient à , et qui vérifie la condition initiale :
, et qui vérifie la condition initiale :  = 0 $) .
.
Donc, cette primitive est : = \int_{\pi}^x \sin ( x) dx + R( \pi ) = \int_{\pi}^x \sin ( x) dx + 0 = \int_{\pi}^x \sin (x) dx $) .
.
Maintenant, il te reste à calculer cette intégrale : dx $) .
.
J'imagine que tu sais calculer des integrales, non ?
Cordialement. :happy3:
Pour :
Il existe une infinité de primitives de
Dans le cas de ton exercice, on cherche une seule primitive particulière qui appartient à
Donc, cette primitive est :
Maintenant, il te reste à calculer cette intégrale :
J'imagine que tu sais calculer des integrales, non ?
Cordialement. :happy3:
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
