Bonjour à vous !
Première question : comment mettre des symboles math sur internet, ça clarifirait pas mal :)...
Voici mon problème (je vais encore avoir l'air con...) :
Soit la série de fonction suivante :
f(x)= somme de k=1 jusque l'infini de :
(k+1)^0,5 * (x+3)^k
--------------------
2^k * k
Les questions:
--------------
Dom f ?
Dom de dérivabilité ?
f '(x) ? La série obtenue converge-t-elle en x=-1 ?
Je suis vraiment désolé mais je ne vois pas du tout comment calculer le domaine de f...
Merci
Série de fonction
10 messages
- Page 1 sur 1
par Sdec25 » 09 Aoû 2006, 18:34
Salut
En utilisant le critère de Cauchy (racine nième) on trouve que la série converge pour x compris entre -5 et -1
 = \sum_{k=1}^{+\infty} \frac{\sqrt{k+1} \, (x+3)^k}{k . 2^k} = \sum_{k=1}^{+\infty} u_k (x))
Pour savoir si la série converge pour x=-1, on peut trouver un équivalent.
 = \sum_{k=1}^{+\infty} \frac{\sqrt{k+1} \, 2^k}{k . 2^k}<br />= \sum_{k=1}^{+\infty} \frac{\sqrt{k+1}}{k})
La suite équivaut au voisinage de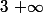
à 
donc la série diverge pour x=-1
D'après mes calculs la série dérivée ne converge pas non plus.
En utilisant le critère de Cauchy (racine nième) on trouve que la série converge pour x compris entre -5 et -1
Pour savoir si la série converge pour x=-1, on peut trouver un équivalent.
La suite équivaut au voisinage de
D'après mes calculs la série dérivée ne converge pas non plus.
par Nic » 09 Aoû 2006, 18:36
Merci à toi thomas 
.
Donc voici ce que j'ai fait, mais y a un truc qui ne va pas:
J'utilise le critère de la racine, on a :
})^1^/^k) * (x+3) ) }{( 2 * \sqrt[k]{k})})
En mettant en évidence k et en le sortant de la racine, on a après simplification :
On peut encore dire que la limite en +
de 1/2k vaut 0. On a donc :
La série sera convergente si ce résultat est inférieur à 1 et divergente si plus gd que 1. Si c'est égal à 1 alors on ne sait pas dire.
Voilà c'est là que je suis bloqué. Merci de me donner un petit coup de pouce
Bonne Soirée
.Donc voici ce que j'ai fait, mais y a un truc qui ne va pas:
J'utilise le critère de la racine, on a :
En mettant en évidence k et en le sortant de la racine, on a après simplification :
On peut encore dire que la limite en +
La série sera convergente si ce résultat est inférieur à 1 et divergente si plus gd que 1. Si c'est égal à 1 alors on ne sait pas dire.
Voilà c'est là que je suis bloqué. Merci de me donner un petit coup de pouce
Bonne Soirée
par nekros » 09 Aoû 2006, 18:39
Oui, il suffit de trouver un équivalent et de s'apercevoir que c'est une série de Riemann avec 1/2 < 1 donc diverge.
Scdec > j'aboutis au même résultat pour la série dérivée.
Nic > tu cherches à utiliser le critère de D'Alembert, c'est bien ça ?
Thomas G :zen:
Scdec > j'aboutis au même résultat pour la série dérivée.
Nic > tu cherches à utiliser le critère de D'Alembert, c'est bien ça ?
Thomas G :zen:
par nekros » 09 Aoû 2006, 18:43
Nic,
Tu cherches à utiliser le critère de d'Alembert, c'est bien ça ?
Dans ce cas, il faut étudier
avec 
le terme général de la série.
Thomas G :zen:
Tu cherches à utiliser le critère de d'Alembert, c'est bien ça ?
Dans ce cas, il faut étudier
Thomas G :zen:
par Nic » 10 Aoû 2006, 07:01
Alors Thomas, ce n'est pas le critère d'alembert non... Par contre, c'est bien celui de la racine comme l'a dit Sdec25. J'ai écrit mon message en même temps que toi Sdec25 lol.
Tes réponses sont correctes: la suite est convergente entre -5 et -1 et divergente en -1 par contre semi convergente en -5. Je ne comprend pas comment tu arrives à cet intervalle.
Je suis à . D'après ce critère la série ne converge que si ce nombre est plus petit que 1. Donc,
^k)
, ce qui correspond à une série alternée... en remarquant que ^k = (-1)^k * 2^k)
. De là, il faut étudier la série des modules. On tombe sur une série de rieman avec 
= 1/2 < 1 donc elle diverge... cependant, elle peut être semi-convergente. Pour cela, il faut montrer que 
ou alors calculer la dérivée et montrer qu'elle décroit. Je ne vois pas comment faire cela...
En ce qui concerne le domaine de dérivabilité, comment le calculer? Simplement en "ouvrant" les crochets ? Alors là je vais avoir l'air con, mais pourquoi ouvre-t-on les crochets? Question de continuité je pense ?
Merci à vous deux !
Tes réponses sont correctes: la suite est convergente entre -5 et -1 et divergente en -1 par contre semi convergente en -5. Je ne comprend pas comment tu arrives à cet intervalle.
Je suis à
En ce qui concerne le domaine de dérivabilité, comment le calculer? Simplement en "ouvrant" les crochets ? Alors là je vais avoir l'air con, mais pourquoi ouvre-t-on les crochets? Question de continuité je pense ?
Merci à vous deux !
par Sdec25 » 10 Aoû 2006, 13:23
Pourquoi on prend la valeur absolue ?
Le critère de Cauchy (comme celui de D'Alembert) permet de comparer la série avec une série géométrique.
La racine énième donne la raison de cette série.
Si la raison est supérieure à 1 en valeur absolue alors la série diverge.
Si la raison est inférieure à 1 en valeur absolue la série converge. Cela marche aussi pour des raisons négatives, par exemple : somme des (-1/2)^n converge.
Donc on prend toujours la valeur absolue pour le critère de Cauchy, il faut que la racine énième soit comprise entre -1 et 1 (exclu ou inclu ça dépend, car pour 1 et -1 on ne peut pas conclure).
Si la racine énième vaut 1, on ne peut pas dire si la série diverge ou converge.
Pour trouver le domaine de dérivabilité il suffit d'appliquer le critère sur la série dérivée (somme des termes dérivés de la suite).
Le critère de Cauchy (comme celui de D'Alembert) permet de comparer la série avec une série géométrique.
La racine énième donne la raison de cette série.
Si la raison est supérieure à 1 en valeur absolue alors la série diverge.
Si la raison est inférieure à 1 en valeur absolue la série converge. Cela marche aussi pour des raisons négatives, par exemple : somme des (-1/2)^n converge.
Donc on prend toujours la valeur absolue pour le critère de Cauchy, il faut que la racine énième soit comprise entre -1 et 1 (exclu ou inclu ça dépend, car pour 1 et -1 on ne peut pas conclure).
Si la racine énième vaut 1, on ne peut pas dire si la série diverge ou converge.
Pour trouver le domaine de dérivabilité il suffit d'appliquer le critère sur la série dérivée (somme des termes dérivés de la suite).
par Nic » 10 Aoû 2006, 13:34
Oui c'est ce que j'ai fait plus haut . Merci pour le module ...
Sinon la série est semi-convergente en -5... tout comme la série harmonique alternée. Comment peut-on le détecter? J'ai proposé en haut deux méthodes (celle avec la dérivée et une autre), est-ce bien cela qu'il faut faire?
Concernant la dérivabilité, on dérive simplement et ensuite on tire le domaine à ce moment alors. Il n'est donc pas question d'ouvrir simplement les crochets, même si cela marche ici . Donc, dériver, appliquer les critères et voir le domaine si j'ai bien compris.
. Merci pour le module ...Sinon la série est semi-convergente en -5... tout comme la série harmonique alternée. Comment peut-on le détecter? J'ai proposé en haut deux méthodes (celle avec la dérivée et une autre), est-ce bien cela qu'il faut faire?
Concernant la dérivabilité, on dérive simplement et ensuite on tire le domaine à ce moment alors
. Il n'est donc pas question d'ouvrir simplement les crochets, même si cela marche ici . Donc, dériver, appliquer les critères et voir le domaine si j'ai bien compris.par Sdec25 » 10 Aoû 2006, 13:59
Les critères de semi-convergence sont : suite alternée et strictement décroissante vers 0 (en valeur absolue).
Tu as vu que^k = (-1)^k 2^k)
donc il reste ^k \, \frac{\sqrt{k+1}}{k})
qui est une suite alternée et décroissante vers 0 en valeur absolue, donc la série est semi-convergente.
Tu as vu que
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :