mathsnico a écrit:Salut Kikoo,
C'est certainement tout l'exercice, mais je vais etre plus precis;
PARTIE A:
1. Dois-je remplacer a et b dans l'algorithme avec ces nombres. Si oui, quelle serait la formule?
2. Je ne comprend pas la question du tout.
3. J'ai des difficultes a faire un algorithme.
4 et 5. Questions tres faciles, mais je dois avoir besoin de la reponse de la question 3, donc je ne demandes pas la reponse a ces questions.
PARTIE B:
Toute la partie est compliquee et imcomprehensible.
Tout d'abord, pour la première question :
Tu effectues la div euclidienne de a par b : ton algorithme prend tout d'abord deux nombres a et b, a>b. Tu soustrais autant de fois que possible la quantité b à a, et tu retournes à chaque fois la valeur du reste de la diveuc' du reste précédent par b. A chaque étape, tu incrémentes le compteur m de 1, qui compte le nombre d'étapes (de soustractions) qui mènent à un reste inférieur à b.
PS : c'est le principe de la méthode de la divisions euclidienne :
Tant que tu n'obtiens pas un reste négatif (dans ton exo) ou un reste inférieur strictement à b et toujours positif, tu répètes l'opération de soustraction de a par b, afin d'obtenir un reste
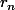
final tel que :

Présentons un exemple :
Faisons la division euclidienne de 94 par 13.
Soustrayons une fois, puis deux, puis trois, ... autant que nécessaire :
94-13=81 et m=1
81-13=68; m:=m+1=2
68-13=55; m:=m+1=3
55-13=42; m:=m+1=4
42-13=29; m:=m+1=5
29-13=16; m:=m+1=6
16-13=3; m:=m+1=7
r=3<13
On stoppe.
Donc au final, 94=7*13+3

