Fonction exponentielle et derivé

[lokstyle]

voila bonjour pourrais-je avoir un calcule detaille de la fonction derivée de : f:x= (e^x)/(1+X) merci!!!

[Carpate]

voila bonjour pourrais-je avoir un calcule detaille de la fonction derivée de : f:x= (e^x)/(1+X) merci!!!

x ou X ?
S'il s'agit de , utilise la formule du cours bien connue des lycéens :

[lokstyle]

c'est ce que j'ai fait mais je ne suis pas sur de ma reponse, j'ai obtenu -e^x/(1+x) mais aller savoir si c correct
il me demande ensuite de determiner le signe de f':x sur ]-1:+ infini[ mais je ne sais pas egalement

[Carpate]

c'est ce que j'ai fait mais je ne suis pas sur de ma reponse, j'ai obtenu -e^x/(1+x) mais aller savoir si c correct
il me demande ensuite de determiner le signe de f':x sur ]-1:+ infini[ mais je ne sais pas egalement

Non c'est faux, donne le détail de ton calcul de dérivée

[lokstyle]

U=e^x U'=e^x
V=1+x V'=1

f':x=((e^x(1+x)-(e^x*1))/(1+x)²
f':x=(e^x(-1+(1+x))/(1+x)²
comme il y a 1 +x au denominateur et numerateur je supprime ceux ci, ce qui enleve le au carré en bas et donne
f':x=(e^x(-1))/(1+X)
f':x=-e^x/(1+x)

[Carpate]

U=e^x U'=e^x
V=1+x V'=1

f':x=((e^x(1+x)-(e^x*1))/(1+x)²
f':x=(e^x(-1+(1+x))/(1+x)² -1+1 donne 0
comme il y a 1 +x au denominateur et numerateur je supprime ceux ci, ce qui enleve le au carré en bas et donne Non !
f':x=(e^x(-1))/(1+X) x est devenu X et (1+x)^2 est devenu 1+X !
f':x=-e^x/(1+x)

Pourquoi marques-tu f'x:x pour f'(x) ç'est incorrect
Donc :;
dérivée qui est du signe de x ...

[lokstyle]

merci vous m'etes d'un grand soutient
a partir de la j'etudie le signe du numerateur et du numerateur pour la suite?

[Carpate]

merci vous m'etes d'un grand soutient
a partir de la j'etudie le signe du numerateur et du numerateur pour la suite?

Quel est le signe de , du numérateur, du dénominateur ?

[lokstyle]

e^x est superieur a 0 et est donc positif sur R
pour x +1, la valeur interdite est positif sur 0: + infini
donc la formule est positive. est-ce ca?

[Carpate]

e^x est superieur a 0 et est donc positif sur R
pour x +1, la valeur interdite est positif sur 0: + infini
donc la formule est positive. est-ce ca?

e^x et (1+x)^2 sont toujours >0 donc f'x) a le signe de x
C'est ce que je t'avais déjà indiqué

[lokstyle]

donc s'il depend de x il est negatif en -1 et positif a partir de 0 jusqu'en + l'infini

[Carpate]

donc s'il depend de x il est negatif en -1 et positif a partir de 0 jusqu'en + l'infini

f(x) et f'(x) ne sont pas définis en -1 !
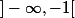
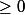
f'(x) est négatif sur et sur ]

[lokstyle]

merci beaucoup et encore une chose comment fait tu les signes mathematiques tels que + infini et tous car cela me permeterai d'etre plus explicite sur internet!

[Kikoo <3 Bieber]

Salut,

merci beaucoup et encore une chose comment fait tu les signes mathematiques tels que + infini et tous car cela me permeterai d'etre plus explicite sur internet!

Pour écrire mathématiquement correct, on utilise le TeX disponible sur ce forum. Tu dois apprendre la syntaxe (voir "pour écrire des belles formules..." dans les différentes sections de ce forum) ce qui est assez rapide, puis tu encadreras ton texte mathématique des bornes [TEX]...[/ TEX] (sans l'espace entre / et TEX)

[lokstyle]

et a la question, montrer que f(x)=2 admet deux soluce sur [-0,9;2]