Série et critère de comparaison

[julien56]

Bonjour

J'arrive pas à faire cet exercice ...

Soit Un une série telle que pour tout n > 0 :

0 < Un < (5/6)^n

Cet encadrement permet il de savoir:

1) Si la suite Un est convergente ? Si oui, quelle est sa limite ?

2) Si la série Un est convergente ? Si oui, quelle est sa limite?

La 1 par contre j'ai pas trop d'idée ... j'aurai dis oui mais sans trop savoir pourquoi

Pour la 2 j'aurai dis que la série converge vers 0 donc cela permet de déterminer que Un est convergent et sa limite est égal à 0

[julien56]

Et pour la suite j'aurai dis qu'elle était croissante est majorée par (5/6)^n finalemenent et donc une suite croissante et majorée est forcement convergente et sa limite est égale à 0 =)

[Gathart]

Salut et bonne année!
C'est un exercice typique :

Je ne vais pas te donner la réponse mais je vais t'aider pour le moment :
Pour qu'une suite soit convergente, on appréci beaucoup avoir des critères de convergences.
1/ Majoré et croissante
2/ Minoré et décroissante
3/ Bornée et monotone
4/ Le théorème des gendarmes c'est à dire borné par deux autres suites convergentes vers une même limite.

Ensuite pour les séries c'est la même chose sauf qu'on ne peut pas conclure sur 1 2 et 3 donc la 4 nous parait judicieux ^^. Donc si tu as un encadrement avec deux series convergentes vers une même limite alors la série va converger.

Réfléchis plus et à suivre...

[Gathart]

Autre chose : majoré, c'est à dire par quelque chose indépendant de n

[julien56]

Salut et bonne année!
C'est un exercice typique :

Je ne vais pas te donner la réponse mais je vais t'aider pour le moment :
Pour qu'une suite soit convergente, on appréci beaucoup avoir des critères de convergence.
1/ Majoré et croissante
2/ Minoré et décroissante
3/ Bornée et monotone
4/ Le théorème des gendarmes c'est à dire borné par deux autres suites convergentes vers une même limite.

Ensuite pour les séries c'est la même chose sauf qu'on ne peut pas conclure sur 1 2 et 3 donc la 4 nous parait judicieux ^^. Donc si tu as un encadrement avec deux series convergente vers une même limite alors la serie va converger.

Réfléchis plus et à suivre...

Personnellement j'aurai dis que la suite est majorée par (5/6)^n et croissante donc en clair elle est convergente ... et que sa limite est égale à 0
Et pour la série, j'aurai dis qu'elle serait aussi convergente car (5/6)^n converge vers 0 donc si les deux côtés convergent vers 0, alors Un converge mais on ne peut rien dire sur sa limite ... Sauf que celle est ci est comprise entre 0 et 6

[Gathart]

Je répète pour :
1/ La suite en n est majorée par un terme dépendant de n et est croissante c'est faux de conclure en disant bah sa converge. Contre-exemple : 0<u_n<n convergente et majoré par pour autant que je sache si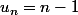 pour 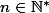sa ne marche pas...

2/Non, tu confonds suite et série (même dans ton énoncé) il faut que la série converge vers 0. C'est à dire .
continue encore un peu tu y es presque ...

[julien56]

Je répète pour :
1/ La suite en n est majorée par un terme dépendant de n et est croissante c'est faux de conclure en disant bah sa converge. Contre-exemple : 0
2/Non, tu confonds suite et série (même dans ton énoncé) il faut que la série converge vers 0. C'est à dire \sum (\frac{5}{6})^n.
continue encore un peu tu y es presque ...


L’énonce est un copié collé de l'exo donné en partiel ...

C'est bizarre pourtant, dans mon polycop de cours, il est marqué qu'une suite majorée et croissance est convergente ...

(5/6)^n converge vers 0 car 5/6 est compris entre -1 et 1 ...

[julien56]

L’énonce est un copié collé de l'exo donné en partiel ...

C'est bizarre pourtant, dans mon polycop de cours, il est marqué qu'une suite majorée et croissance est convergente ...

(5/6)^n converge vers 0 car 5/6 est compris entre -1 et 1 ...

[julien56]

Ahh je crois avoir compris

1) Nous avons une suite croissante et bornée avec x SUPÉRIEUR à 0 (on a ainsi une suite à terme positif) . Nous pouvons en déduire que cette suite est convergente. Sa limite est 0 car (5/6) est compris entre -1 et 1.

2) nous avons une série qui est convergente car (5/6)^n est de la forme q^n avec q compris entre -1 et 1. Sa limite est aussi 0 car (5/6) est compris entre -1 et 1 ...

J'espers que c'est bon ...

[Gathart]

Alalalala c'est presque la bonne réponse.

Pour la 1 on ne peut pas dire que la suite est majorée par car celà dépend de n je le répète encore et encore. En revanche, on peut dire qu'elle est majorée par 1 c'est grossier mais c'est vrai ^^. Mais le seul problème rien nous dis que la suite est croissante donc la bonne réponse est :

- La suite est une suite bornée par deux suites 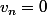et pour tout . Or c'est deux suites converges vers la même limite 0. On en conclut par le théorème des gendarmes que la suite converge vers 0.

Pour la 2 c'est plus subtile, On sait juste que la série de terme général converge vers car c'est une série géométrique. C'est à dire que la série converge vers $6$.
La série de terme général est positif et son terme général est majoré par une suite dont la série est convergente. Donc la série de terme général est convergente.

Attention : Si la série est convergente, alors la suite converge vers 0 mais la réciproque est fausse

Donc ce n'est pas sorcier pour t'aider je te conseille cette page : http://fr.wikipedia.org/wiki/S%C3%A9rie_convergente

Ensuite à faire attention :
On parle de suite
On parle de série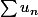
On parle de série de terme général ou encore de la série de
Mais il n'y a pas de sens de dire que est une série à part si on parle de suite de série.

[Gathart]

Ici aussi les notations te sont bien expliquées :
http://fr.wikipedia.org/wiki/S%C3%A9rie_(math%C3%A9matiques)

[julien56]

Okay merci je viens de comprendre mon erreur ...

Je me posais une autre question ... Si on doit calculer la somme d'une série dont les n commence à partir de 2 ou autres chiffres ..

Exemple :

Série dont les n sont supérieur ou égal à 2 => (-3/4)^n

Pour la somme on devra bien faire ceci ?

- -3/4 compris entre -1 et 1

1/(1+3/4) - (-3/4)^0 - (3/4)^1

= 4/7 - 1 - 3/4

soit ici -33/28

C'est bon de dire ça ?

[Gathart]

oui oui ^^
Tu rajoutes les termes qu'il te manque à ta série et tu les enlèves ensuite. Donc c'est bon

[julien56]

D'accord !

Merci beaucoup pour avoir pris le temps de m'aider ...

Je vous souhaite une bonne fin de journée