Vecteur 1ere S
20 messages
- Page 1 sur 1
Vecteur 1ere S
Bonsoir , bonsoir , j'étais entrains de faire une série sur les vecteur quand je suis tombée sur un exercice plutôt dur pour une élève de mon niveau , trêve de bavardage :ptdr: .
J'ai pris le soin de prendre une photo de l'exercice vous la trouverez dans le lien ci-dessous :
http://www.noelshack.com/2013-01-1357328314-iphone-image-01-04-2013.jpg
J'espère que vous allez pouvoir me venir en aide :we: , car là je fonce droit au mur :mur: ... :hein:
Cordialement : Lise , 1ère S .
J'ai pris le soin de prendre une photo de l'exercice vous la trouverez dans le lien ci-dessous :
http://www.noelshack.com/2013-01-1357328314-iphone-image-01-04-2013.jpg
J'espère que vous allez pouvoir me venir en aide :we: , car là je fonce droit au mur :mur: ... :hein:
Cordialement : Lise , 1ère S .
Salut !
1°) Dans ce repère, est l'origine et
est l'origine et  et
et  sont les deux vecteurs élémentaires de ce repère donc pour trouver les coordonnées des points
sont les deux vecteurs élémentaires de ce repère donc pour trouver les coordonnées des points 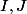 et
et  dans ce repère, il faut exprimer les vecteurs
dans ce repère, il faut exprimer les vecteurs  et
et 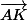 en fonction des deux vecteurs élémentaires
en fonction des deux vecteurs élémentaires  et
et  .
.
En prenant par exemple le point , cela revient à trouver deux réels
, cela revient à trouver deux réels  et
et  tels que
tels que  ; dans ce cas, les coordonnées de
; dans ce cas, les coordonnées de  dans
dans ) seront
seront ) .
.
tequilasunrise a écrit:Bonsoir , bonsoir , j'étais entrains de faire une série sur les vecteur quand je suis tombée sur un exercice plutôt dur pour une élève de mon niveau , trêve de bavardage :ptdr: .
J'ai pris le soin de prendre une photo de l'exercice vous la trouverez dans le lien ci-dessous :
http://www.noelshack.com/2013-01-1357328314-iphone-image-01-04-2013.jpg
J'espère que vous allez pouvoir me venir en aide :we: , car là je fonce droit au mur :mur: ... :hein:
Cordialement : Lise , 1ère S .
1°) Dans ce repère,
En prenant par exemple le point
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
1°) Dans ce repère,est l'origine et
et
sont les deux vecteurs élémentaires de ce repère donc pour trouver les coordonnées des points
et
dans ce repère, il faut exprimer les vecteurs
et
en fonction des deux vecteurs élémentaires
et
.
En prenant par exemple le point, cela revient à trouver deux réels
et
tels que
; dans ce cas, les coordonnées de
dans
seront
.
:ptdr: j'ai compris un peu les démarche mais par exemple pour I(1/2;0) depuis le graphique et meme cas pour k qui aura comme ordonné 1/2 et aussi pour j :hum: ? c'est une méthode faisable ?
tequilasunrise a écrit::ptdr: j'ai compris un peu les démarche mais par exemple pour I(1/2;0) depuis le graphique et meme cas pour k qui aura comme ordonné 1/2 et aussi pour j :hum: ? c'est une méthode faisable ?
Malheureusement, il t'est demandé de calculer ces coordonnées.
On ne pourra donc se contenter d'une vulgaire lecture graphique.
I et J sont graphiquement simple à trouver mais K ?
Il faut pour cela te servir des informations données dans l'énoncé :
1°) Pour
Pour
Enfin pour
:++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Malheureusement, il t'est demandé de calculer ces coordonnées.
On ne pourra donc se contenter d'une vulgaire lecture graphique.
I et J sont graphiquement simple à trouver mais K ?
Il faut pour cela te servir des informations données dans l'énoncé :
1°) Pour, utilise le fait que
est milieu de
;
Pour,
;
Enfin pour,
:++:
Par exemple pour trouver J on peut faire : que on a A(0;0) et C (0,1) donc AC(0;1) et AC + CJ = JC donc on a et Cj (1.25,1/2 ) c'est possible ?
:hum: ?
tequilasunrise a écrit:Par exemple pour trouver J on peut faire : que on a A(0;0) et C (0,1) donc AC(0;1) et AC + CJ = JC donc on a et Cj (1.25,1/2 ) c'est possible ?
:hum: ?
Ton raisonnement est faux.
Puis d'ailleurs, d'après le dessin, tu devrais pouvoir voir directement que l'abscisse du point J dans le repère est nulle.
Fait comme je te l'ai dit :
Exprimer
Pour cela, part la relation
D'après Chasles,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Ton raisonnement est faux.
Puis d'ailleurs, d'après le dessin, tu devrais pouvoir voir directement que l'abscisse du point J dans le repère est nulle.
Fait comme je te l'ai dit :
Exprimeren fonction de
et
.
Pour cela, part la relation.
D'après Chasles,donc ...
Après 10 minute de réflexion je conclu ça :
JC = JA +AC
donc on a AC(1;0)
et JC 5 JA donc J(1.25;0)
tequilasunrise a écrit:Après 10 minute de réflexion je conclu ça :
JC = JA +AC
donc on a AC(1;0)
et JC 5 JA donc J(1.25;0)
Je ne comprends pas ta réponse... :hum:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
tequilasunrise a écrit:Après 10 minute de réflexion je conclu ça :
JC = JA +AC
donc on a AC(1;0)
et JC 5 JA donc J(1.25;0)
capitaine nuggets a écrit:Je ne comprends pas ta réponse... :hum:
tequilasunrise a écrit:c'est évident ; du moins je crois que c'est évident uh on a JC = 5 JA donc 1/5JC=JA on a A(0;0) C(1;0) donc 1/5 = 0.25 j(0;1+0.25) = J(0;1;25)
C'est logique non :ptdr: ?
Je suis désolé, mais si on relis ton premier post, il n'était pas tout à fait très clair.
De plus, ne dis pas que c'est évident alors que tu me proposes comme première réponse J(1.25;0) puis une deuxième J(0;1;25) en me disant que c'est logique.
De toute évidence, tu n'as pas l'air très sûre de ton résultat.
Contente-toi de trouve les coordonnées de J vectoriellement.
Ca me fait penser, pourrais-tu me montrer comment tu as trouvé les coordonnées de I ?
On devrait peut-être commencer par là, vu que tu ne m'as pas montré.
Parce que, si tu ne sais pas trouver les coordonnées de I vectoriellement, il y a bien peu de chance que tu y arrives avec J, et ne parlons pas de K.
:we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
tequilasunrise a écrit:bah pour I ; c'est facile , on a i Milleu de AB donc AI+IB= AB donc I(1/2;0)
Le résultat est peut-être juste mais le raisonnement ne l'est pas.
Je te l'ai dit :
Exprime
Tu as su trouver graphiquement que
(Là j'ai tout dit quasiment).
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Le résultat est peut-être juste mais le raisonnement ne l'est pas.
Je te l'ai dit :
Exprimeen fonction des deux vecteurs élémentaires du repère :
et
.
Tu as su trouver graphiquement quedonc
s'exprimera uniquement en fonction de
.
(Là j'ai tout dit quasiment).
On AC + 2AI = AB
tequilasunrise a écrit:On AC + 2AI = AB
Bon, je crois que je vais te montrer une démonstration à titre d'exemple :
I est le milieu de [AB] donc
Et là, c'est fini : on a exprimé
Combien de fois y a-t-il le vecteur
Combien de fois y a-t-il le vecteur
conclusion : Dans le repère
Je te laisse faire de même avec les deux autres :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Bon, je crois que je vais te montrer une démonstration à titre d'exemple :
I est le milieu de [AB] donc.
Et là, c'est fini : on a expriméen fonction de
et
.
Combien de fois y a-t-il le vecteur?
fois ;
Combien de fois y a-t-il le vecteur?
fois.
conclusion : Dans le repère,
admet pour coordonnées
.
Je te laisse faire de même avec les deux autres :+++:
ok je vais essayer ; c'est surtout que mes lacunes sont du a mon absence lors des cours sur les vecteur en classe , c'est pour ça que je suis aussi nul que sans parler que lundi a 10 heures j'ai un Ds ou je vais devoirs revoir de cruelles vecteur partout :mur:
capitaine nuggets a écrit:Bon, je crois que je vais te montrer une démonstration à titre d'exemple :
I est le milieu de [AB] donc.
Et là, c'est fini : on a expriméen fonction de
et
.
Combien de fois y a-t-il le vecteur?
fois ;
Combien de fois y a-t-il le vecteur?
fois.
conclusion : Dans le repère,
admet pour coordonnées
.
Je te laisse faire de même avec les deux autres :+++:
On 5JC = JA donc 1/5JC =JA
Combien de fois y a-t-il le vecteur AB ? 0 fois .
Combien de fois y a-t-il le vecteur AC ? 1fois et 1/4 donc
J admet pour cordonnées (1;1/2)
biensûr, en regardant ton dessin, tu as vu immédiatement que c'était faux 
Mais ne désespère pas :we:
Rappelle-toi ce que j'ai dis hier soir :
Mais ne désespère pas :we:
Rappelle-toi ce que j'ai dis hier soir :
capitaine nuggets a écrit:(...)
Puis d'ailleurs, d'après le dessin, tu devrais pouvoir voir directement que l'abscisse du point J dans le repère est nulle.
Fait comme je te l'ai dit :
Exprimeen fonction de
et
.
Pour cela, part de la relation.
D'après Chasles,donc ...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
