Le polynome d'interpolation de Lagrange
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mekkadra
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Déc 2011, 18:13
-
 par Mekkadra » 03 Jan 2013, 15:15
par Mekkadra » 03 Jan 2013, 15:15
Bonsoir jeunes
Construire le polynome d'interpolation de Lagrange
)
pour une fonction continue définie
sur léintervalle [-1,1] en utilisant les pois d'interpolation x0=-1 ; x1=1
- montrer que si la seconde dérivée de f existe et continue sur [-1,1],alors :
-p_{1}(x) \right |)
<=
)
<=

- Ou
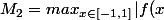}''\right | \\)
. Donner un exemple de fonction f et un point x pour lequel on aura égalté.
MERCI D'AVANCE . ..
-
Mekkadra
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Déc 2011, 18:13
-
 par Mekkadra » 03 Jan 2013, 15:27
par Mekkadra » 03 Jan 2013, 15:27
je fait la premiere question suivre moi :
=\frac{x-1}{-2})
=\frac{x+1}{2})
=f(-1)l_0(x)+f(1)l_1(x)=-f(-1)\frac{x-1}{2}+f(1)\frac{x+1}{2}})
[/B]
-
Mekkadra
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Déc 2011, 18:13
-
 par Mekkadra » 03 Jan 2013, 15:31
par Mekkadra » 03 Jan 2013, 15:31
Aider moi sur question 2 !!
je avais la solution avec le théorème de Rolle !!
mai . . .
..........
.......
Voici la façon dont étudiés
*-Méthode de sustitutions successives(poins-fixe).
*-Méthode de point fixe.
C'est ce que je devrais utiliser pour résoudre l'exercice . . . !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités