étude de suite

[biomel]

Bonjour à tous,

Je bloque sur un exercice de suite.

Voici l'énoncé :
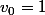
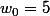
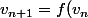et et et

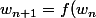Je dois indiquer sur un graphique les premiers termes de ces suites.
Puis montrer que est croissante et majorée par 4.

Je pense que si je me débloque sur ce début je pourrait faire la suite.

Ce que je ne comprend pas c'est qu'on ne donne pas la raison du coup je n'arrive pas à placer les points.

Merci d'avance.

[Manny06]

Bonjour à tous,

Je bloque sur un exercice de suite.

Voici l'énoncé :
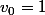
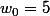
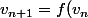et et et

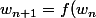Je dois indiquer sur un graphique les premiers termes de ces suites.
Puis montrer que est croissante et majorée par 4.

Je pense que si je me débloque sur ce début je pourrait faire la suite.

Ce que je ne comprend pas c'est qu'on ne donne pas la raison du coup je n'arrive pas à placer les points.

Merci d'avance.

connais tu la fonction f ?

[biomel]

connais tu la fonction f ?

Justement la première partie s'agissait d'étudier la fonction f(x) = 2+lnx

Vous croyez que c'est cette fonction f ?

[biomel]

J'ai fais mes calculs avec cette fonction ! je pense qu'il y a que cette solution ! Merci

[biomel]

J'ai reussie à m'avancer dans l'exercie mais je bloque sur la dernière question.

Soit l=lim . Quelle équation vérifie l ?
Justifier que l>= 1 . Trouver l. Procéder de même pour

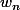
Je pense utiliser ce théorème : Si est convergente et si lim =l et si f continue en l, alors le nombre l est solution de l'équation f(x)=x

Je pense qe si je comprend pour je pourrait faire pour !

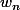
Merci d'avance

[Manny06]

J'ai reussie à m'avancer dans l'exercie mais je bloque sur la dernière question.

Soit l=lim . Quelle équation vérifie l ?
Justifier que l>= 1 . Trouver l. Procéder de même pour

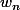
Je pense utiliser ce théorème : Si est convergente et si lim =l et si f continue en l, alors le nombre l est solution de l'équation f(x)=x

Je pense qe si je comprend pour je pourrait faire pour !

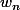
Merci d'avance

effectivement c'est ce théorème qu'il faut appliquer
dans l'étude de la fonction f as-tu cherché les points d'intersection avec la droite d'équation y=x
il y en a un d'abscisse inferieure à 1 et l'autre d'abscisse supérieure à 3
v0=1 et vn croissante donc l>=1