Polynôme orthogonaux - Legendre -

[Nikki]

salut ,

Dans le cours des polynômes orthogonaux on a vu les fonctions du poids , défini dans le produit scalaire dans l'espace E :
Supposons maintenant qu'on connait K(t)=1 (fonction poids de legendre )
On me demande de prouver que les polynômes de lengendre ont une forme générale de :
Pn(x)=

[mathelot]

bonjour,
il convient de séparer existence et unicité d'une telle base:

i) l'existence est donnée par le procédé d'orthogonalisation de la base
canonique par Gram-Schmidt
ii) Une telle base orthogonale est unique , à un facteur près, bien que la démonstration
ne m'en saute pas aux yeux (admis)

maintenant avec ces résultats de cours, il reste à considérer deux polynomes
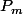
et de Legendre, de considérer leur produit scalaire
de faire une intégration par parties pour montrer que
(symbole de Kronecker)

réel.

Par intégration par parties, on devine que l'on va obtenir
la dérivée 2n-ième d'un polynome de degré 2n, les termes de bord s'annulant
si n=m, zéro sinon car l'intégrale d'une dérivée n-ième d'un polynome de degré m avec n>m.

cordialement,