Trouver les bijections dérivables
Equation fonctionnelle
11 messages
- Page 1 sur 1
Equation fonctionnelle
(Je vous en prie, inutile de me féliciter pour l'originalité de mon titre)
Trouver les bijections dérivables de
de  vérifiant
vérifiant 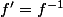 .
.
Trouver les bijections dérivables
Bonjour !
J'ai essayé de voir ça et je n'ai trouvé aucune fonction vérifiant cela pour l'instant.
vérifiant cela pour l'instant.
A mon avis, il n'y a aucune solution (ai-je bon ?).
J'ai essayé de voir ça et je n'ai trouvé aucune fonction
A mon avis, il n'y a aucune solution (ai-je bon ?).
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
si on cherche les solutions analytiques il doit pas y en avoir beaucoup.
A part 0, f a un autre point fixe ; autour de ce point fixe on peut faire le DL de f et à partir de f sur un intervalle ouvert autour du point fixe, on en déduit f partout.
Donc selon le point fixe on a une unique solution analytique.
Mais je doute que toutes ces solutions aterrissent à (0,0). Donc doit y en avoir qu'une qui soit analytique (celle qu'on a déjà trouvée).
A part 0, f a un autre point fixe ; autour de ce point fixe on peut faire le DL de f et à partir de f sur un intervalle ouvert autour du point fixe, on en déduit f partout.
Donc selon le point fixe on a une unique solution analytique.
Mais je doute que toutes ces solutions aterrissent à (0,0). Donc doit y en avoir qu'une qui soit analytique (celle qu'on a déjà trouvée).
Salut,
On pourrait peut-être ici se servir de la densité des fonctions analytiques dans l'ensemble des fonctions dérivables (qui découle du théorème de Stone-Weierstrass).
Ainsi, si f vérifie cette équa-diff, on peut trouver une suite de fonctions Fn analytiques, qui convergent (au sens d'une norme bien choisie) vers f. Et montrer qu'à partir d'un certain rang elles sont très proches de la solution analytique du problème (et donc que cette solution est une valeur d'adhérence de la suite). On en déduirait que f ne pourrait être que cette fonction analytique.
Ça vous semble faisable ?
Je vois bien comme norme N, si on appelle M la norme uniforme N(f)=M(f')+M(f)
p-s. Par analytique j'entends somme de puissances non nécessairement entières
On pourrait peut-être ici se servir de la densité des fonctions analytiques dans l'ensemble des fonctions dérivables (qui découle du théorème de Stone-Weierstrass).
Ainsi, si f vérifie cette équa-diff, on peut trouver une suite de fonctions Fn analytiques, qui convergent (au sens d'une norme bien choisie) vers f. Et montrer qu'à partir d'un certain rang elles sont très proches de la solution analytique du problème (et donc que cette solution est une valeur d'adhérence de la suite). On en déduirait que f ne pourrait être que cette fonction analytique.
Ça vous semble faisable ?
Je vois bien comme norme N, si on appelle M la norme uniforme N(f)=M(f')+M(f)
p-s. Par analytique j'entends somme de puissances non nécessairement entières
Allez hop, je met le plan de la solution (dsl d'avoir laissé moisir le topic)
Soit assez grand. On vérifie sans peine que
assez grand. On vérifie sans peine que >M) . Soit
. Soit  une constante telle que
une constante telle que \leq Cx) pour
pour 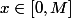 (
( existe car
existe car =0) )..
)..
On en déduit alors que\geq \frac{x}{C}) pour
pour ]) , donc pour
, donc pour 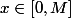 . Ce qui donne donc
. Ce qui donne donc \geq \frac{x}{C}) donc, en intégrant entre 0 et x,
donc, en intégrant entre 0 et x, \geq \frac{x^2}{2C}) pour
pour 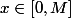 .
.
Puis on poursuis la même méthode:\geq \frac{x^2}{2C}) donc
donc =f^{-1}(x)\leq \sqrt{2Cx}) donc intégrant
donc intégrant \leq \frac{2\sqrt{2C}}{3}x^{\frac{3}{2}}) .
.
En poursuivant ce procédé, on définit deux suites) et
et ) par des relations de reccurence explicites, telles que
par des relations de reccurence explicites, telles que \leq A_nx^{B_n}) si n pair,
si n pair, \geq A_nx^{B_n}) si n impair. (pour
si n impair. (pour 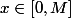 )
)
Une petite étude de suite plus loin, on constate que) et
et ) convergent vers des réels A, B absolus(correspondant à la solution trouvée queques posts plus haut), et on conclut ainsi que
convergent vers des réels A, B absolus(correspondant à la solution trouvée queques posts plus haut), et on conclut ainsi que =Ax^B) pour tout
pour tout 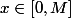 , puis pour tout
, puis pour tout 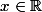 , M étant arbitraire.
, M étant arbitraire.
Soit
On en déduit alors que
Puis on poursuis la même méthode:
En poursuivant ce procédé, on définit deux suites
Une petite étude de suite plus loin, on constate que
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
