Soient a, b et c trois réels strictements positifs tels que
Inégalité a,b,c>0
23 messages
- Page 1 sur 2 - 1, 2
Inégalité a,b,c>0
Bonjour, voici une jolie inégalité :
Soient a, b et c trois réels strictements positifs tels que(b+c)(c+a)=1) . Montrer que :
. Montrer que :
 .
.
Soient a, b et c trois réels strictements positifs tels que
Bonsoir, j'ai peut-être un semblant de réponse.
Il faut avant tout remarquer qu'un produit de trois termes ne peut-être égal à 1 que si un ou deux de ces termes seulement sont inférieurs à 1.
En effet si tous les termes sont strictements supérieurs à 1, leur produit ne peut-être égal 1 et inversement, si tous les termes sont strictement inférieurs à 1, leur produit ne peut être égal à 1.
Plus clairement, il faut distinguer deux cas :
- Un terme est supérieur ou égal à 1, les deux autres sont inférieurs ou égaux à 1
- Deux termes sont supérieurs ou égaux à 1, l'autre est inférieur ou égal à 1
Ces trois termes ont ici un rôle symétrique, c'est à dire que choisir que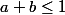 reviens au même que si l'on choisissait
reviens au même que si l'on choisissait 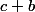 ou
ou 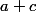 .
.
(b+c)(a+c)=1)
(bc+ab+c^2+ac)=1)
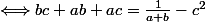 car
car 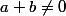
---------------------------------------------------------------------
1er cas :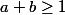 ,
, 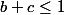 ,
, 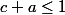 (arbitrairement)
(arbitrairement)
Par addition membre à membre des inégalités,
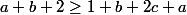
D'où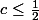
--------------------------------------------------------------------
2ème cas :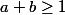 ,
, 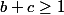 ,
, 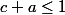 (arbitrairement)
(arbitrairement)
De ces inégalités, on obtient par addition et soustraction :
-(b+c)+1\ge1-1+(c+a))
D'où, après simplification,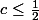
--------------------------------------------------------------------
Dans les deux cas, on a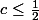
Il en vient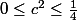 (1)
(1)
Or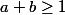
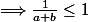 (2)
(2)
De (1) et (2) on tire ainsi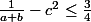
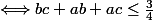
Bonne nuit !
Il faut avant tout remarquer qu'un produit de trois termes ne peut-être égal à 1 que si un ou deux de ces termes seulement sont inférieurs à 1.
En effet si tous les termes sont strictements supérieurs à 1, leur produit ne peut-être égal 1 et inversement, si tous les termes sont strictement inférieurs à 1, leur produit ne peut être égal à 1.
Plus clairement, il faut distinguer deux cas :
- Un terme est supérieur ou égal à 1, les deux autres sont inférieurs ou égaux à 1
- Deux termes sont supérieurs ou égaux à 1, l'autre est inférieur ou égal à 1
Ces trois termes ont ici un rôle symétrique, c'est à dire que choisir que
---------------------------------------------------------------------
1er cas :
Par addition membre à membre des inégalités,
D'où
--------------------------------------------------------------------
2ème cas :
De ces inégalités, on obtient par addition et soustraction :
D'où, après simplification,
--------------------------------------------------------------------
Dans les deux cas, on a
Il en vient
Or
De (1) et (2) on tire ainsi
Bonne nuit !
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
