Espace de fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 17 Déc 2012, 20:02
par zork » 17 Déc 2012, 20:02
Bonjour,
dans un espace de fonction continue, quelle est la définition d'une suite de Cauchy
est ce:
pour tout
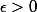
, il existe no dans N, pour tout n dans N, n>=no=>

merci
-
Yann64
- Membre Naturel
- Messages: 55
- Enregistré le: 03 Oct 2012, 15:42
-
 par Yann64 » 17 Déc 2012, 20:13
par Yann64 » 17 Déc 2012, 20:13
pour tout epsilon > 0 il existe n_0 dans IN pour tous p,q >= n_0

-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 17 Déc 2012, 20:18
par zork » 17 Déc 2012, 20:18
j'ai pensé au début que c'était ca
mais après j'ai eu un doute puisque dans un exo, on emploie la définition que j'ai donné
gn dans C^1([-1,1],R)
gn(x)=(nx²)/2 +1/(2n) si |x|<1/n
|x| si x>=1/n
Montrer que (gn) est de cauchy
-
sabaga
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Oct 2011, 20:50
-
 par sabaga » 17 Déc 2012, 21:39
par sabaga » 17 Déc 2012, 21:39
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 18 Déc 2012, 09:34
par Doraki » 18 Déc 2012, 09:34
C'est quoi f dans la définition que t'as donnée ?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 18 Déc 2012, 14:57
par zork » 18 Déc 2012, 14:57
c'était la limite de la suite (fn)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 18 Déc 2012, 15:05
par zork » 18 Déc 2012, 15:05
A sabaga
aurait on pu majorer comme cela:
<=|(qx²)/2+1/2q|<=(qx²+1)/2
du coup pour avoir
/2< \epsilon)
on choisit
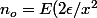+1)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 19 Déc 2012, 14:38
par zork » 19 Déc 2012, 14:38
en faites, pour
gn dans C^1([-1,1],R)
gn(x)=(nx²)/2 +1/(2n) si |x|<1/n
|x| si x>=1/n
on montrer qu'elle converge uniformément vers |x| et du coup elle est de cauchy
mais comment trouve-t-on le sup|gn(x)-|x||
dans la correction on dit que c'est 1/(2n) mais comment on l'a trouvé?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Déc 2012, 14:46
par Doraki » 19 Déc 2012, 14:46
Peut-être en étudiant la fonction gn(x) - |x| sur [-1;1]
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 19 Déc 2012, 14:54
par zork » 19 Déc 2012, 14:54
oui
mais on ne peut pas étudier ces variations à cause de |x|
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 19 Déc 2012, 15:03
par Doraki » 19 Déc 2012, 15:03
je vois pas en quoi ça gêne ?
Tu peux étudier séparément sur [-1;0] et sur [0;1] et recoller à la fin.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 19 Déc 2012, 15:07
par zork » 19 Déc 2012, 15:07
oui c'est vrai
merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités