Exo de denombrabilité

par **takow** » 09 Déc 2012, 21:03

Bonjour ;
je me suis bloqué sur une question d un exo
montrer que A={n²/n de |N} est denombrable
merci d avance

par **cuati** » 09 Déc 2012, 21:10

takow a écrit:Bonjour ;
je me suis bloqué sur une question d un exo
montrer que A={n²/n de |N} est denombrable
merci d avance

Ton ensemble A est indexé par

, fin de la démonstration... :lol3:

par **takow** » 09 Déc 2012, 21:19

-Pour dire que N² est dénombrable je dis que puisque l'application est une bijection |N²| = |N| et puisque N est dénombrable N² l'est également.
n est ce pas ?

par **cuati** » 09 Déc 2012, 21:27

takow a écrit:-Pour dire que N² est dénombrable je dis que puisque l'application est une bijection |N²| = |N| et puisque N est dénombrable N² l'est également.
n est ce pas ?

Hou-là ! minute !
Tu veux montrer que A est dénombrable ou alors tu veux montrer que

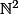
est dénombrable ? C'est pas pareil !
Pour A, je t'ai fait une "démonstration" précédemment mais pour

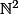
... tu peux montrer par exemple que

est une bijection de

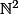
vers

par **takow** » 09 Déc 2012, 21:34

nn pardon moi je voulais juste montrer que A est Denombrable : donc il suffit de dire que puisque n de N sachant que ce dernier est denombrable donc A qui est index par N est denombrable
c est ca ?

Exo de denombrabilité

exo de denombrabilité

Qui est en ligne