Triangle équilatéral nombres complexes

[charchour]

Bonjour, je suis en train de faire plein d'exos sur les nombres complexes, mais il y en a 5 parmi qui me posent difficulté. Je vous montre le premier et ce que j'ai fait.

1. Déterminer l’ensemble des points M du plan d’affixe z ;) C, tels que z, z^2 et z^3 soient les affixes
d’un triangle équilatéral.

ce que j'ai fait
z^2-z= e^(ipi/3) (z^3-z)
qui signifie que z^2 est l'image de z^3 dans la rotation de centre z et d'angle pi/3.
z^2= [( 1+i racine(3))/2] * (z^3-z) + z
(a+ib)^2= [( 1+i racine(3))/2] ((a+ib)^3 - (a+ib))
en mettant de l'autre côté, en développant, et séparant les X d'avec les Y dans X+Yi
j'ai
(a^3) /2+ a-a^2+b^2+ [(a^3racine(3))/2 + 3a^2b-3b^2a-b^3+b-2ab] i

mais après il faut que je trouve le a et le b. Il aurait fallu faire une double équation, mais je ne sais pas comment faire.
Sinon il y a l'égalité des modules |z^2-z|= |z^3-z|=|z^3-z|
avec z= a+ib
z^2= a^2-b^2 + 2abi
z^3= a^3-3ab^2 + (3a^2b- b^3) i
par contre est-ce que l'expression de mon z^3 est bonne pour entreprendre d'autres calculs par le moyen des modules pour mon triangle équilatéral?

Voilà je vous remercie d'avance

[chan79]

salut
Ecris que |z-z²|=|z-z³|=|z²-z³|
tu auras rapidement les 4 possibilités pour z (2 seulement donnent un "vrai" triangle)

[Anonyme]

@charchour

C'est juste un commentaire sur la manière dont tu as écrit les indices des affixes de 2 de tes 3 points

Le point M_2 a pour affixe z_2 ( et non pas z^2 )

Regarde ce que cela "donne" en mettant juste "les balises LATEX" dans la phrase précédente :
Le point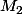 a pour affixe 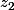( et non pas )

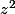Si tu n'utilises pas le codage LATEX alors par convention :
La notation x^2 veut dire x au carré
La notation x_2 veut dire le nombre x_2

ps)
"les balises LATEX" sont : [ TEX] ...... [/TEX]
avec le T de TEX collé au [

[Xulthiar]

Tu peux sinon passer par les racines troisièmes de l'unité, qui par définition, forment un triangle équilatéral.
(Elles sont , et )