DM sur les statistiques

[Naais04]

On considère la série statistiques formée des nombres 2, 3 et 5.
On note d la fonction de dispersion de cette série et f la fonction de dispersion des écarts absolus :
d(x)=1/3[(x1-x)²+(x2-x)²+(x3-x)² et f(x)=(|x1-x|+|x2-x|+|x3-x|)

1. Déterminer l'expression de d sous forme développéé, puis montrer que d admet son minimum pour la moyenne de la série.

2/ a) Ecrire l'expression de f(x) sur chacun des intervalles suivants :]-l'infini;2], [2;3[, [3;5[ et [5; +l'infini[

b) Représenter la fonction f dans un repère du plan pour x appartient [-4;10]

c) En déduire que f admet son minimum pour la médiane de la série.

Pour cette partie je n'y arrive vraiment pas, j'ai essayer de développer mais j'arrive pas jusqu'au bout et les autres questions sont du chinois ...


On considère une série statistiques x1, x2,....,xn de moyenne x(avec la barre dessus). Soit D la fonction définie sur tout les réels par :
D(x) = 1/N [(x1-x)² + (x2+x)² + ... + (xn-x)²]

1. Vérifier que D est une fonction trinôme du second degré
2. On pose : D(x) = ax²+bx+c
Justifier que l'on a : a=1/n ; b= -2x(avec la barre dessus); c=1/n(x1²+x2²+...+xn²)
3. Dresser le tableau de variation de D.
Préciser la valeur du minimum de D ainsi que la valeur pour laquelle il est atteint.

Je suis juste perdue ... Si vous pouviez me donner des pistes :$ . Merci d'avance!

[Sylviel]

1) Pour d il faut trouver son minimum, pour cela une étude de fonction rapide s'impose :
calcul de dérivée
étude du signe de la dérivée
tableau de variation
conclusion sur le minimum.

2 a) tu sais que |A|=A si A>=0, ou -A si A<0. Sur les intervalles que l'on t'indique tu peux réécrire ainsi la fonction f.

[Anonyme]

@Naais04

Quelques explications supplémentaires :

Comme x1=2 et x2=3 et x3=5

- la fonction d est définie par d(x)=1/3[(2-x)²+(3-x)²+(5-x)²]

- et la fonction f est définie par f(x)=1/3(|2-x|+|3-x|+|5-x|)

la fonction d est une fonction de la famille des fonctions du type d(x)=ax²+bx+c

La fonction f , à cause des valeurs absolues , n'est pas la même sur les intervalles : ]-l'infini;2], [2;3[, [3;5[ et [5; +l'infini[

Par exemple
si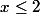 |2-x|=2-x
si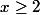 |2-x|=x-2