Je veux déterminer l'équation des tangentes à une ellipse passant par le point de coordonnées
L'ellipse a pour équation :
Avec a=3 et b=2.
Quelquun aurait une piste ?
romain.autret a écrit:Bonjour,
Je veux déterminer l'équation des tangentes à une ellipse passant par le point de coordonnées(0,2)
L'ellipse a pour équation :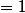
Avec a=3 et b=2.
Quelquun aurait une piste ?
OUI et alors le pointromain.autret a écrit:Jai oublié de préciser que l'ellipse a pour centre (0,-2)
OUIromain.autret a écrit:Cela revient a résoudre un systeme ?
chan79 a écrit:salut
sans doute (x,y) sinon le point serait à l'intérieur de l'ellipse
ptitnoir a écrit:@Black Jack
Je suis OK avec cette deuxième méthode (que je trouve moins "élégante"),
ce qui est normal : car je préfère forcément MA méthode car c'est la MIENNE !
ptitnoir a écrit:@Black Jack
Si tu le dis je te crois car je n'ai fait aucun calcul
et j'ai raisonné par rapport à un dessin que j'ai fait à la main levé
Donc tu as certainement raison
Cependant ( je pense ) qu'on peut appliquer ces 2 méthodes
( mais ma méthode devient d'un seul coup beaucoup moins élégante qu'avant...)
A l'auteur de cette discussion d'appliquer ces 2 méthodes s'il le souhaite
A+
ptitnoir a écrit:@Black Jack
Merci pour ton message
ps)
quelle méthode préfères tu ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :