Fonctions

[loubna0302]

Bonjour, est ce que vous pourriez m'aider pour mon exercice de maths s'il vous plaît ?

Soit f la fonction f définie sur R par f(x)= 4x²+24x+11

1) Dresser un tableau de valeurs de -8 à 2
c'est fait

2) Construire la courbe
(c'est fait )

3) Dresser le tableau de variations de F sur R à partir de la courbe.
C'est la que ça coince parce que je ne sais pas comment faire étant donné que la courbe est infinie

4) Faire le tableau de signe de F
Pareil que la question précédente.

5 ) F admet -elle des extremums sur R ? En quelles valeurs sont ils atteints ?

Elle admet bien un extremum qui ici est un minimum. Le minimum sur [-8;2] de f est -25 atteint pour x= -3. Est ce correct ?


Merci d'avance.

[Rockleader]

Pour ta question 3, commence par étudier le signe de la dérivé de ta fonction.

[homeya]

Bonjour,

Pour la question 3), F étant la primitive, f sera sa fonction dérivée. Donc, lorsque f sera positive, F sera croissante et lorsque f sera négative, F sera décroissante.

Cordialement.

[mcar0nd]

Bonjour tout le monde,

Je pense pas qu'il y a besoin des dérivées et des primitives dans cette exo.
loubna0302 doit être en première, auquel cas, elle doit savoir donner le sens de variations et le signe d'un trinôme juste en connaissant son expression. ;)

[Rockleader]

Le programme de 1ère sauf s'il a changé entre temps, c'était en plein là dedans

Donner les variations d'une fonction en étudiant le signe de sa dérivé.

[homeya]

Si c'est du programme de première, alors F ne serait pas la primitive de f (ce que je pensais initialement). Qu'en pensez-vous ?

[mcar0nd]

Le programme de 1ère sauf s'il a changé entre temps, c'était en plein là dedans

Donner les variations d'une fonction en étudiant le signe de sa dérivé.

Bah je suis en première en ce moment, et on doit savoir donner le signe et les variations d'un trinôme seulement en connaissant son expression, en fonction de la valeur du coefficient devant .

Si c'est du programme de première, alors F ne serait pas la primitive de f (ce que je pensais initialement). Qu'en pensez-vous ?

Je pense aussi que F n'est pas la primitive.

[Rockleader]

Si c'est du programme de première, alors F ne serait pas la primitive de f (ce que je pensais initialement). Qu'en pensez-vous ?

Clairement erreur de frappe, les primitives c’est pour la terminale, ici il faut comprendre F=f enfin je pense.

Bah je suis en première en ce moment, et on doit savoir donner le signe et les variations d'un trinôme seulement en connaissant son expression, en fonction de la valeur du coefficient devant .

Puisque le programme semble avoir changé, je vous laisse le guider avec les notions du cours de première actuel.

[mcar0nd]

Puisque le programme semble avoir changé, je vous laisse le guider avec les notions du cours de première actuel.

On voit encore les dérivées en première mais c'est après les polynômes de degré 2 donc il faut savoir faire ça sans les dérivées.

[loubna0302]

Ok, merci j'ai compris. Pourriez vous m'aider s'il vous plait pour la fin de l'exercice maintenant ?

Démontrer que pour tout x réel, f(x)=4(x+3)²-25
(fait)

Déterminez le ou les antécédents de -25 par f

Et la je n'y arrive pas :mur:

[mcar0nd]

Ok, merci j'ai compris. Pourriez vous m'aider s'il vous plait pour la fin de l'exercice maintenant ?

Démontrer que pour tout x réel, f(x)=4(x+3)²-25
(fait)

Déterminez le ou les antécédents de -25 par f

Et la je n'y arrive pas :mur:

Tu dois résoudre .

[loubna0302]

Non non je suis en seconde, et oui F= f désolé erreur de frappe

[mcar0nd]

Non non je suis en seconde, et oui F= f désolé erreur de frappe

D'accord, donc il fallait que tu fasse tout ça graphiquement alors je suppose.
Trace ta courbe et regarde les variations et le signe pour pouvoir rentrer tout ça dans un tableau.
Pour les variations, elle "fait" quoi ta courbe?

[loubna0302]

Tu dois résoudre .

4(x+3)²-25=-25
4(x+3)²=0

C'est la que ca bloque car je voulais résoudre une équation de produit nul mais je n'y arrive pas.

[mcar0nd]

4(x+3)²-25=-25
4(x+3)²=0

C'est la que ca bloque car je voulais résoudre une équation de produit nul mais je n'y arrive pas.

C'est bien une équation de produit nul donc tu ne peux avoir que .

[loubna0302]

D'accord, donc il fallait que tu fasse tout ça graphiquement alors je suppose.
Trace ta courbe et regarde les variations et le signe pour pouvoir rentrer tout ça dans un tableau.
Pour les variations, elle "fait" quoi ta courbe?

ma courbe est une parabole mais c'est bon je pense avoir réussi. J'ai fais:

x: -infini -3 +infini

f(x): (fleche qui descend) -25 (fleche qui monte)

[mcar0nd]

ma courbe est une parabole mais c'est bon je pense avoir réussi. J'ai fais:

x: -infini -3 +infini

f(x): (fleche qui descend) -25 (fleche qui monte)

Oui, c'est juste.

[loubna0302]

C'est bien une équation de produit nul donc tu ne peux avoir que .

Je ne comprends pas pourquoi le 4 disparait et le + se tranforme en - . Pourrais tu m'expliquer stp ?

[mcar0nd]

Je ne comprends pas pourquoi le 4 disparait et le + se tranforme en - . Pourrais tu m'expliquer stp ?

Le + qui devient - c'est que j'ai fais une erreur de frappe, excuse moi.

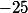
Donc tu dois résoudre soit donc là tout de suite, tu remarques que les s'annulent et il te reste qui est une équation de produits nuls ( de la forme ) donc il faut que l'un au moins des facteurs soient nuls or 4 il ne peut pa changer, il sera toujours différent de zéro. Donc pour que il faut que .