Suites

[marievlan]

Soit une suite réelle telle que , . Est ce que la est nécessairement convergente ? Si oui, le démontrer ; sinon, donner un contre exemple.



Quelqu'un peut t'il m'aider ???!

[Nightmare]

Hello,

regarde par exemple U(n)=ln(n).

[marievlan]

Je ne vois pas ce que ça me donne....

[Nightmare]

Que vaut la limite de U(n+p)-U(n) pour p quelconque?

[marievlan]

et sa limite est bien 0 quand n tend vers l'infini.... OK !

[marievlan]

Merci !!!!

[Nightmare]

Je t'en prie.

[Mathusalem]

@Night,

Comment procéderais-tu pour trouver facilement d'autres contre-exemples ? Je ne sais pas si c'est un problème classique, mais j'aurais mis un moment avant de trouver ln(n) comme contre-exemple.

[Nightmare]

L'hypothèse implique en particulier que si la suite diverge, alors cette divergence est nécessairement très lente.

J'ai donc simplement cherché parmi les suites à divergence très lente que je connaissais, ln(n) est la première, par chance elle marche.

La deuxième que je connais est la série harmonique, par chance elle marche aussi ^^

[cuati]

J'ajouterai que pour une suite qui tend vers l'infini, comme l'a écrit Nightmare, la divergence est lente au sens ou implique que la suite tend vers l'infini de moins en moins "vite"... Il existe beaucoup de fonction de ce type, en est une autre...

[Nightmare]

Oui tient, rac(n) marche aussi mais je la trouvais pas assez lente pour la considérer :we:

[Nightmare]

Et si on remplace U(n+p) par U(pn)?

[cuati]

Et si on remplace U(n+p) par U(pn)?

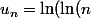:lol3:

[Nightmare]

Ca me va! :happy2:

[Nightmare]

Et le dernier : U(n^p)-U(n) tend vers 0 ? :lol2:

(Une fois qu'on a compris...)

[cuati]

Et le dernier : U(n^p)-U(n) tend vers 0 ? :lol2:

(Une fois qu'on a compris...)

On peut continuer longtemps comme ça :ptdr:

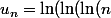[Nightmare]

héhé :zen:

Bon, et si on en trouvait une qui, cette fois-ci, assure la convergence?

[Skullkid]

héhé :zen:

Bon, et si on en trouvait une qui, cette fois-ci, assure la convergence?

Autre que le critère de Cauchy ?

[cuati]

héhé :zen:

Bon, et si on en trouvait une qui, cette fois-ci, assure la convergence?

Hmmm, très bonne question :we:
Je vais y réfléchir, tout ce que je sais dans ce genre là est valable pour une suite récurrente :
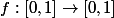
Si est continue et alors on a l'équivalence entre converge et

[Nightmare]

Autre que le critère de Cauchy ?

Le critère de Cauchy n'est pas "fonctionnel".

Ce que je voudrais, c'est une fonction f : NxN -> N si possible pas trop moche telle que :
(pour tout p, u(f(n,p))-u(n) tend vers 0) => (u(n) converge)

Le critère de Cauchy ne nous fournit pas une telle fonction f.