Densité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 18 Nov 2012, 16:15
par majin » 18 Nov 2012, 16:15
bonjour,j'ai un peu du mal sur cet exo qui n'est pas évident (je voudrais qu'un indice):
Construire

telle que

et
l'ensemble des

tel que
)
ne tend pas vers

est dense dans

merci
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 18 Nov 2012, 16:24
par Skullkid » 18 Nov 2012, 16:24
Bonjour, déjà est-ce que tu me donner un ensemble dense dans [0,1] ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 18 Nov 2012, 16:47
par cuati » 18 Nov 2012, 16:47
Bonjour,
une autre idée : découper [0,1] en des intervalles de plus en plus petits.
=\mathcal{1}_{[\frac{k}{2^n},\frac{k+1}{2^n}]}(x))
avec
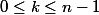
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 18 Nov 2012, 19:07
par majin » 18 Nov 2012, 19:07
Skullkid a écrit:Bonjour, déjà est-ce que tu me donner un ensemble dense dans [0,1] ?
J'ai pensé à
,n\in\mathbb{N} \right \})
, mais je vois pas le rapport
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 18 Nov 2012, 19:08
par majin » 18 Nov 2012, 19:08
cuati a écrit:Bonjour,
une autre idée : découper [0,1] en des intervalles de plus en plus petits.
=\mathcal{1}_{[\frac{k}{2^n},\frac{k+1}{2^n}]}(x))
avec
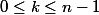
C'est ce que j'ai essayé de faire au début, et je ne comprend pas très bien ta fonction
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 18 Nov 2012, 19:24
par Skullkid » 18 Nov 2012, 19:24
majin a écrit:J'ai pensé à
,n\in\mathbb{N} \right \})
, mais je vois pas le rapport
Cet ensemble n'est pas dense dans [0,1]. Normalement le tout premier exemple de densité qu'on rencontre c'est Q dans R. De la même manière, l'ensemble E des rationnels de [0,1] est dense dans [0,1].
Essaye de construire une suite constante de fonctions qui satisfait l'énoncé à l'aide de cet ensemble E.
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 18 Nov 2012, 21:55
par majin » 18 Nov 2012, 21:55
=x)
si

dans

=1/n)
sinon
mais cette fonction n'est même pas continue par morceaux
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 18 Nov 2012, 22:34
par Skullkid » 18 Nov 2012, 22:34
majin a écrit:=x)
si

dans

=1/n)
sinon
mais cette fonction n'est même pas continue par morceaux
Oui, ou plus simplement fn(x) = 1 si x est dans E, 0 sinon. L'énoncé que tu as donné ne demande pas que les fn soient continues par morceaux.
-
majin
- Membre Naturel
- Messages: 83
- Enregistré le: 12 Nov 2011, 21:30
-
 par majin » 18 Nov 2012, 22:45
par majin » 18 Nov 2012, 22:45
Skullkid a écrit:Oui, ou plus simplement fn(x) = 1 si x est dans E, 0 sinon. L'énoncé que tu as donné ne demande pas que les fn soient continues par morceaux.
Mais je crois que pour intégrer f, il faut qu'elle soit continue par morceaux
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 18 Nov 2012, 23:02
par Skullkid » 18 Nov 2012, 23:02
majin a écrit:Mais je crois que pour intégrer f, il faut qu'elle soit continue par morceaux
En toute généralité, non, mais si ton cours ne parle que de l'intégration des fonctions continues par morceaux alors il vaut en effet mieux s'y tenir. La piste proposée par cuati te fournit une suite de fonctions continues par morceaux, en prenant comme ensemble dense
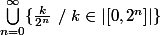
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
, mais je vois pas le rapport