Isomorphisme de corps

[mirlamber]

Bonjour

Soit P = x² + x + 2 et Q = y² + 2y + 2

Ces 2 polynomes sont irréductibles

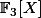
Je dois montrer que les corps /(P) et /(Q) sont isomorphes en construisant un isomorphisme

Je n'ai pas trop d'idée
merci d'avance

[Doraki]

Tu peux toujours énumérer tous les éléments de F3[X]/(P) (il y en a seulement 9) et en chercher un qui est une racine du polynôme Q.

[mirlamber]

Justement mon probleme c'est que je n'arrive pas à écrire les éléments de F3/(P)
Est ce que vous pouvez me dire comment ils s'écrivent ?

[Doraki]

ce sont les classes de polynômes modulo 3 et X²+X+2.

Tout polynôme A à coefficients dans F3 peut s'écrire de manière unique sous la forme A = QP + R où Q est un polynôme quelconque et R est un polynôme de degré < degré de P = 2 (par l'algorithme de la division euclidienne)
Donc dans chaque classe cl(A) il y a un unique représentant de degré < 2, le polynôme R dans A = QP+R.
Réciproquement chaque polynome de degré < 2 est dans une classe bien à lui, donc pour avoir tes éléments il faut juste écrire tous les polynomes de degré < 2.

[mirlamber]

Le polynome est plutot de degré strictement inférieur à 2 non ? puisque P est de degré 2

Dans ce cas je dirai que les éléments de F3/(P) s'écrivent donc
0, - 1, 1, x, x + 1 et x - 1 non ?

Q étant aussi de degré 2, alors les éléments de F3/(Q) c'est exactement les memes ?!

[Skullkid]

Bonjour, une autre façon de voir les choses, moins rigoureuse que celle donnée par Doraki. L'ensemble K[X]/(P) peut se voir comme l'ensemble des objets que tu peux construire à partir des trois ingrédients suivants :

- les éléments de K
- un nouvel élément X qui satisfait P(X) = 0
- les opérations de corps de K

Par exemple si on prend K = R le corps des réels et P = X²+1, on obtient le corps des complexes, qui est bien le corps des réels auquel on a ajouté un nouvel élément X (communément noté i) qui vérifie X²+1 = 0.

[Doraki]

oui pardon.
Par contre il te manque -x, -x+1, et -x-1 dans tes représentants.

Et non c'est pas la même chose parcequ'ils se multiplient pas de la même façon.
Si tu prends la classe de x dans F3[x]/P,
tu as cl(x)*cl(x) = cl(x*x) = cl(x²) = cl(x² - P) = cl(-x+1)

Si tu prends la classe de y dans F3[y]/Q,
tu as cl(y)*cl(y) = cl(y*y) = cl(y²) = cl(y² - Q) = cl(y+1)

[mirlamber]

oui pardon.
Par contre il te manque -x, -x+1, et -x-1 dans tes représentants.

Et non c'est pas la même chose parcequ'ils se multiplient pas de la même façon.
Si tu prends la classe de x dans F3[x]/P,
tu as cl(x)*cl(x) = cl(x*x) = cl(x²) = cl(x² - P) = cl(-x+1)

Si tu prends la classe de y dans F3[y]/Q,
tu as cl(y)*cl(y) = cl(y*y) = cl(y²) = cl(y² - Q) = cl(y+1)

Oui je comprends mieux merci
Mais je ne comprends l'égalité souligné :/

[mirlamber]

Bonjour, une autre façon de voir les choses, moins rigoureuse que celle donnée par Doraki. L'ensemble K[X]/(P) peut se voir comme l'ensemble des objets que tu peux construire à partir des trois ingrédients suivants :

- les éléments de K
- un nouvel élément X qui satisfait P(X) = 0
- les opérations de corps de K

Par exemple si on prend K = R le corps des réels et P = X²+1, on obtient le corps des complexes, qui est bien le corps des réels auquel on a ajouté un nouvel élément X (communément noté i) qui vérifie X²+1 = 0.

Justement la question qui suit est : construire un autre isomorphisme différent du premier
Il y a un truc qui je comprends pas, aucun éléments de F3[X] ne satisfait P = 0

[Doraki]

J'ai juste changé de représentant dans la classe de x² dans F3[X]/P.
La classe de x² dans F3[X]/P c'est l'ensemble des polynomes B tels que B-x² est multiple de P.
x²-P est dedans parceque (x²-P)-x² = (-1)*P, qui est un multiple de P.
Donc x² et x²-P sont dans la même classe d'équivalence :
La classe de x² dans F3[X]/P = la classe de x²-P dans F3[X]/P

[Doraki]

Justement la question qui suit est : construire un autre isomorphisme différent du premier
Il y a un truc qui je comprends pas, aucun éléments de F3[X] ne satisfait P = 0

Si, la classe de x dans F3[X]/P satisfait P(cl(x)) = 0.

[mirlamber]

J'ai juste changé de représentant dans la classe de x² dans F3[X]/P.
La classe de x² dans F3[X]/P c'est l'ensemble des polynomes B tels que B-x² est multiple de P.
x²-P est dedans parceque (x²-P)-x² = (-1)*P, qui est un multiple de P.
Donc x² et x²-P sont dans la même classe d'équivalence :
La classe de x² dans F3[X]/P = la classe de x²-P dans F3[X]/P

Ah oui d'accord, moi je faisais comme ça
x² = P.Q + R : Q = 1 et R = -x + 1
ce qui revient donc au meme puisque Q = 1

[Doraki]

oui ça revient au même, c'est juste que là j'avais la flemme de dire que je faisais l'algorithme de division et j'ai tout de suite sorti le bon quotient.

[mirlamber]

oui ça revient au même, c'est juste que là j'avais la flemme de dire que je faisais l'algorithme de division et j'ai tout de suite sorti le bon quotient.

Je vois
J'ai essayé de choisir le morphisme qui envoye x sur y, x + 1 sur y + 1 etc.. ça ne marche pas car on a pas
si on note f le morphisme, f(ab) = f(a)f(b)

[Doraki]

Bah oui, Q(y)=0 alors que Q(x) = x.

Il faut chercher un élément z de F3[x]/P tel que Q(z)=0, et dire que tu envoies y sur z.

[mirlamber]

Bah oui, Q(y)=0 alors que Q(x) = x.

Il faut chercher un élément z de F3[x]/P tel que Q(z)=0, et dire que tu envoies y sur z.

ooooh d'acc ! je ne l'avais pas vu comme ça, j'ai toujours du mal à manipuler les éléments des ensembles de type F3/(P)

je cherche le morphisme
Merci de vos explications

[mirlamber]

j'ai trouvé que Q(x + 1) = 0

donc le morphisme qui envoye x sur y - 1 convient je pense ?

[mirlamber]

Ah non c'est faux mais j'ai compris pourquoi je vais corriger

[mirlamber]

Bon bah en fait je trouve pas

[Doraki]

moi j'ai que Q(x+1)=0