A l'aide

par **william_z** » 27 Juil 2006, 19:50

exercice sur les variables aleatoires :

Soit fn une fonction sur [0,1] définie par :
fn(x) = b(1-x)^n
ou n N

Donner la valeur de b en fonction de n pour que fn soit une fonction de densite. En particulier pour n=0 ,n=1 et n=2

Merci de bien vouloir m'aider

par **raptor77** » 27 Juil 2006, 19:55

un bonjour serait le bienvenu et mets un titre explicite stp

par **Sdec25** » 27 Juil 2006, 20:11

Si je ne confonds pas, l'intégrale d'une densité de probabilité vaut 1.
L'intégrale de ta fonction sur [0,1] est égale à

donc b=n+1

par **raptor77** » 27 Juil 2006, 20:13

je comprends pas comment on peut répondre à ce genre de question

par **haydenstrauss** » 27 Juil 2006, 20:33

pour qu'une fonction soir une fonction de densité il faut qu'elle soit continue et que son intégral soit égal a 1.

est dérivable et donc continue.

=

or

donc

=

come il faut que l'intégral soit égal a 1 on a :

=

donc

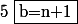
donc pour

on a :

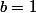
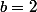
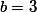
enfin ce message c'est pas dans superieur qu'il faut le mettre c'est dans lycée...
et puis oui un petit bonjour et un merci serai cool

par **raptor77** » 27 Juil 2006, 20:34

Moi je veux un bonjour

par **phoebe** » 27 Juil 2006, 20:37

Bonsoir,

Raptor77 à raison, une certaine politesse est demandée lorsque l'on demande de l'aide :hum:

A+

par **haydenstrauss** » 27 Juil 2006, 20:43

c'est je donne une solution detaillé sans avoir eu de bonjour...

je suis trop gentil

A l'aide

a l'aide

Qui est en ligne