Dénombrement
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Adoration_For_None » 17 Nov 2012, 22:09
par Adoration_For_None » 17 Nov 2012, 22:09
Bonsoir,
Je sollicite votre aide car je bloque depuis un petit moment sur cet exercice :
On pose

le nombre de 3-cycles (a,b,c) définis sur [[1,n]].
La question posée est la suivante :
Pour
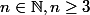
, donner le nombre de 3-cycles f définis sur [[1,n+1]] tels que
\neq n+1)
.
En déduire que :
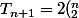+T_n)
puis que
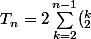)
.
Mon raisonnement :
Si
\neq n+1)
alors

et il faut donc que je choisisse 2 autres
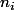
parmi les n éléments restants dans [[1,n+1]]. J'ai
)
choix.
Et je ne vois plus comment avancer... Un indice ?

Merci d'avance !
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 17 Nov 2012, 22:31
par cuati » 17 Nov 2012, 22:31
Adoration_For_None a écrit:... et il faut donc que je choisisse 2 autres
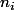
parmi les n éléments restants dans [[1,n+1]]. J'ai
)
choix...
Dans un sens et dans l'autre aussi... :lol3:
 par Adoration_For_None » 17 Nov 2012, 22:37
par Adoration_For_None » 17 Nov 2012, 22:37
Quand tu dis "dans un sens et dans l'autre" c'est pour justifier le
)
, non ?
Mais, je ne vois pas ce que tu sous entends par "sens" ? :/
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 17 Nov 2012, 22:49
par cuati » 17 Nov 2012, 22:49
Adoration_For_None a écrit:Quand tu dis "dans un sens et dans l'autre" c'est pour justifier le
)
, non ?
Mais, je ne vois pas ce que tu sous entends par "sens" ? :/
En fait tu sais que ton 3-cycle envoie (n+1) ailleurs, donc ce 3-cycle est de la forme (n+1,a,b). C'est pour cela que tu choisis deux autres éléments (a et b) parmi les n restants, mais cela n'est pas suffisant pour les compter tous, en effet le 3-cycle (n+1,a,b) n'est pas le même que le 3-cycles (n+1,b,a) (son inverse), autrement dit, l'ordre à une importance dans le choix des 2 autres éléments.
A chaque fois que tu choisis deux éléments a et b il y a deux possibilités de 3-cycles, les deux sus-mentionnés, d'où le 2 devant dans
)
...
 par Adoration_For_None » 17 Nov 2012, 22:55
par Adoration_For_None » 17 Nov 2012, 22:55
Merci beaucoup, je n'avais pas pris en compte cette question d'ordre !
Mais, rien n'oblige mon 3-cycle d'être de la forme (n+1,a,b) ? Donc pourquoi je ne dénombre pas les trois cycles de la forme (a,n+1,b) ou (a,b,n+1), ... ?
Il doit y avoir autre chose qui m'échappe. Désolé. :/
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 17 Nov 2012, 23:03
par cuati » 17 Nov 2012, 23:03
Adoration_For_None a écrit:Merci beaucoup, je n'avais pas pris en compte cette question d'ordre !
Mais, rien n'oblige mon 3-cycle d'être de la forme (n+1,a,b) ? Donc pourquoi je ne dénombre pas les trois cycles de la forme (a,n+1,b) ou (a,b,n+1), ... ?
Il doit y avoir autre chose qui m'échappe. Désolé. :/
Attention : (n+1,a,b)=(a,b,n+1)=(b,n+1,a). Il n'y a en fait que 2 sens possibles avec 3 éléments.
 par Adoration_For_None » 17 Nov 2012, 23:12
par Adoration_For_None » 17 Nov 2012, 23:12
N'ayant pas encore vu les cycles en cours, je ne comprends pas bien pourquoi on a ces résultats...
Dans mon exercice ils sont simplement définis par :
un 3-cycle (abc) est l'application de E dans E définie par
f(a)=b, f(b)=c, f(c)=a et pour

f(x)=x.
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 17 Nov 2012, 23:19
par cuati » 17 Nov 2012, 23:19
Adoration_For_None a écrit:N'ayant pas encore vu les cycles en cours, je ne comprends pas bien pourquoi on a ces résultats...
Dans mon exercice ils sont simplement définis par :
un 3-cycle (abc) est l'application de E dans E définie par
f(a)=b, f(b)=c, f(c)=a et pour

f(x)=x.
Oui, (abc) est une notation pour dire que "a" est envoyé en "b", "b" en "c" et "c" en "a", les autres étant fixés. Mais du coup, on a bien (abc)=(bca) non ? et même (abc)=(bca)=(cab).
 par Adoration_For_None » 17 Nov 2012, 23:27
par Adoration_For_None » 17 Nov 2012, 23:27
cuati a écrit:Oui, (abc) est une notation pour dire que "a" est envoyé en "b", "b" en "c" et "c" en "a", les autres étant fixés. Mais du coup, on a bien (abc)=(bca) non ? et même (abc)=(bca)=(cab).
D'accord, ce qui justifie que les deux cycles possibles à trois éléments a,b,c sont (abc) et (acb).
Et d'où je dois dénombrer (n+1,a,b) et (n+1,b,a).
Merci beaucoup !

Donc
)
représente le nombre de 3-cycles f définis sur [[1,n+1]] avec n+1 appartenant au support (c'est comme ça qu'on l'appelle ?) du 3-cycle ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 17 Nov 2012, 23:34
par cuati » 17 Nov 2012, 23:34
Adoration_For_None a écrit:D'accord, ce qui justifie que les deux cycles possibles à trois éléments a,b,c sont (abc) et (acb).
Et d'où je dois dénombrer (n+1,a,b) et (n+1,b,a).
Merci beaucoup !

Donc
)
représente le nombre de 3-cycles f définis sur [[1,n+1]] avec n+1 appartenant au support (c'est comme ça qu'on l'appelle ?) du 3-cycle ?
T'as tout compris :++:
 par Adoration_For_None » 17 Nov 2012, 23:47
par Adoration_For_None » 17 Nov 2012, 23:47
Merci encore !

Et de là, les 3-cycles définis sur [[1,n+1]] correspondent aux 3-cycles définis sur [[1,n]] et aux 3-cycles définis de [[1,n+1]] avec n+1 appartenant au support. En effet, les 3-cycles définis sur [[1,n+1]] peuvent être séparés en deux catégories, ceux intégrant n+1 à leur support (calculé avant) et ceux ne l'intégrant pas, ces derniers étant aussi nombreux que les trois cycles définis sur [[1,n]], on étend juste ces trois cycles sur [[1,n+1]] avec f(n+1)=n+1.
Alors
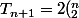+T_n)
.
C'est bon ?

-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 17 Nov 2012, 23:49
par cuati » 17 Nov 2012, 23:49
Oui, c'est nickel :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
, non ?
f(x)=x.
représente le nombre de 3-cycles f définis sur [[1,n+1]] avec n+1 appartenant au support (c'est comme ça qu'on l'appelle ?) du 3-cycle ?