Somme de cardinaux
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Nov 2012, 20:47
par Zweig » 10 Nov 2012, 20:47
Salut,
Soit

un ensemble à

éléments,

. Déterminer, sans récurrence, les sommes suivantes :
)
)
Par exemple, si

alors
 = \text{card}\,\left(\left{1\right}\right) + \text{card}\,\left(\left{2\right}\right) + \text{card}\,\left(\left{3\right}\right) +\text{card}\,\left(\left{1,\,2\right}\right) + \text{card}\,\left(\left{1,\,3\right}\right) +\text{card}\,\left(\left{1,\,2,\,3\right}\right) + \text{card}\,\left(\left{2,\,3\right}\right))
Soit,
 = 12)
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 10 Nov 2012, 22:31
par vincentroumezy » 10 Nov 2012, 22:31
Salut !
Je propose
1)

-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 11 Nov 2012, 01:12
par Zweig » 11 Nov 2012, 01:12
Ouep, et qui vaut ? ;)
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 11 Nov 2012, 04:20
par MMu » 11 Nov 2012, 04:20
Zweig a écrit:Salut,
Soit

un ensemble à

éléments,

. Déterminer, sans récurrence, les sommes suivantes :
)
)
Par exemple, si

alors
 = \text{card}\,\left(\left{1\right}\right) + \text{card}\,\left(\left{2\right}\right) + \text{card}\,\left(\left{3\right}\right) +\text{card}\,\left(\left{1,\,2\right}\right) + \text{card}\,\left(\left{1,\,3\right}\right) +\text{card}\,\left(\left{1,\,2,\,3\right}\right) + \text{card}\,\left(\left{2,\,3\right}\right))
Soit,
 = 2^n)
=\sum_{k=0}\,\text{card}\,(X)2^n)
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 11 Nov 2012, 04:21
par MMu » 11 Nov 2012, 04:21
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 11 Nov 2012, 04:47
par Zweig » 11 Nov 2012, 04:47
Salut,
Nope, c'est
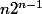
, mais je suppose une faute de frappe, les calculs étant bons.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 11 Nov 2012, 09:06
par fatal_error » 11 Nov 2012, 09:06
salut,
pour la 2 :
pour i=1 a n (taille de l'intersection)
on construit E : k elem parmi (n-i) pour k=0 à n-i
pour ce E donné on construit F : j elem parmi (n-k-i) pour j=0 à n-k-i
ce qui donne
\\<br />S = \bigsum_{i=1}^n iC(n,i)\bigsum_{k=0}^{n-i}C(n-i,k)\bigsum_{j=0}^{n-k-i}C(n-k-i,j)\\<br />S = \bigsum_{i=1}^n iC(n,i)\bigsum_{k=0}^{n-i}C(n-i,k) 2^{n-k-i}\\<br />S = \bigsum_{i=1}^n iC(n,i)2^{n-i}\bigsum_{k=0}^{n-i}C(n-i,k) (\frac{1}{2})^k\\<br />S = \bigsum_{i=1}^n iC(n,i)2^{n-i}(1+\frac{1}{2})^{n-i}\\<br />S = \bigsum_{i=1}^n iC(n,i)3^{n-i}\\)
Si on pose
3^{n-i})
et qu'on dérive et évalue en i, on obtient S, donc
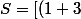^n]' = n4^{n-1})
la vie est une fête

-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 11 Nov 2012, 09:49
par vincentroumezy » 11 Nov 2012, 09:49
Zweig a écrit:Ouep, et qui vaut ?

^n=\sum_{k=0}^n C^{k}_{n} x^k)
On dérive:
^{n-1}=\sum_{k=1}^n k C^{k}_{n} x^{k-1})
L'évaluation en x=1 donne

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 11 Nov 2012, 10:41
par Kikoo <3 Bieber » 11 Nov 2012, 10:41
Hello,
On a :
 \\<br />=\sum_{X\in\mathcal{P}(E)}\text{card}\,(X)\\<br />=\sum_{k=0}^{n}\sum_{X/\text{card}\,(X)=k}\text{card}\,(X)\\<br />=\sum_{k=0}^{n}kC^k_n\\<br />=n\sum_{k=0}^n C^{k-1}_{n-1}\\<br />=n\sum_{k=0}^{n-1} C^{k}_{n-1}\\<br />=n2^{n-1})
si je me suis pas trompé.
Edit : ouaip ou comment reprendre ce qu'a dit Vincentroumezy ^^
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 11 Nov 2012, 11:03
par vincentroumezy » 11 Nov 2012, 11:03
Oui, mais tu as calculé la somme différemment !
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 11 Nov 2012, 11:57
par acoustica » 11 Nov 2012, 11:57
cardinaux J'en compte dix.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Nov 2012, 13:56
par Doraki » 11 Nov 2012, 13:56
Pour tout x de E, l'application qui à une partie X de E contenant x associe X' = X \{x} est une bijection dans l'ensemble des parties de E\{x}, donc :
 \\ =<br />\sum_{x\in E} 2^{n-1} \\ =<br />2^{n-1} \sum_{x \in E} 1 \\ =<br />n 2^{n-1})
Et de même,
^2 \\ =<br />\sum_{x\in E} 2^{2n-2} \\ =<br />2^{2n-2} \sum_{x \in E} 1 \\ =<br />n 2^{2n-2})
Sinon en termes de probabilités, un élément x a une chance sur 2 d'être dans un ensemble X choisi au hasard uniformément dans P(E), donc l'espérance de la taille d'un ensemble choisi au hasard vaut 1/2 * n, mais ceci n'est rien d'autre que (la première somme)/2^n.
Et on fait pareil pour le 2 en prenant deux ensembles X et Y choisis au hasard uniformément et indépendemment dans P(E)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 11 Nov 2012, 14:06
par Zweig » 11 Nov 2012, 14:06
Ouep, vous avez tout bon !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Nov 2012, 14:16
par Nightmare » 11 Nov 2012, 14:16
Hello,
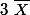
désigne le complémentaire dans E :
=\Bigsum_{X\subset E}\;Card(\bar{X}))
Mais
+Card(\bar{X})=n)
donc
=\Bigsum_{X\subset E} n)
ie
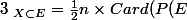)=n.2^{n-1})
.
De même, on a la partition suivante :
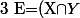\cup(X\cap \bar{Y})\cup(\bar{X}\cap Y)\cup(\bar{X}\cap \bar{Y}))
Mais là encore la somme pour (X,Y) variant dans P(E)² de chaque terme de la partition est égale à la somme des X inter Y.
On a donc
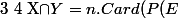^{2}))
et on trouve
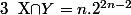
:happy3:
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 11 Nov 2012, 19:45
par MMu » 11 Nov 2012, 19:45
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités