Petit problème..
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 18:44
par Cercle » 08 Nov 2012, 18:44
Bonsoir, voila je n'arrive pas a résoudre cette équation :
4(x+2)²-9(3-2x)²=0
Merci de votre aide ! :hein:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 18:45
par Carpate » 08 Nov 2012, 18:45
Cercle a écrit:Bonsoir, voila je n'arrive pas a résoudre cette équation :
4(x+2)²-9(3-2x)²=0
Merci de votre aide ! :hein:
Factorise :
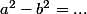
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 18:47
par Cercle » 08 Nov 2012, 18:47
Euh.. Comment ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 18:56
par Carpate » 08 Nov 2012, 18:56
Cercle a écrit:Euh.. Comment ?
A quoi est égal
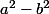
?
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 18:59
par Cercle » 08 Nov 2012, 18:59
Euh, aucune idée..
-
Backtrack
- Membre Naturel
- Messages: 21
- Enregistré le: 12 Sep 2012, 20:03
-
 par Backtrack » 08 Nov 2012, 19:06
par Backtrack » 08 Nov 2012, 19:06
(identités remarquables)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 19:08
par Carpate » 08 Nov 2012, 19:08
Cercle a écrit:Euh, aucune idée..
Je ne sais pas en quelle classe tu es mais si tu ne sais pas (ou n'as pas appris) les bases , notamment les identités remarquables, tu n'as aucune chance de résoudre cet exercice.
 (a+b))
Et maintenant identifie a et b dans l'équation à résoudre :
^2-9(3-2x)^2=0)
a =...
b = ...
puis applique cette factorisation.
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 19:08
par Cercle » 08 Nov 2012, 19:08
Oui sous cette forme : a²-b²=(a+b)(a-b)
Mais je n'y arrive pas
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 19:12
par Cercle » 08 Nov 2012, 19:12
A= 4(x+2)² ?
B= 9(3-2x)² ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 19:12
par Carpate » 08 Nov 2012, 19:12
Cercle a écrit:Oui sous cette forme : a²-b²=(a+b)(a-b)
Mais je n'y arrive pas
^2-9(3-2x)^2=0)
Réponds à ces 2 questions :
^2)
est le carré de ... ?
^2)
est le carré de ... ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 19:16
par Carpate » 08 Nov 2012, 19:16
Cercle a écrit:A= 4(x+2)² ?
B= 9(3-2x)² ?
Non, c'est
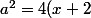^2)
donc

^2)
donc
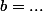
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 19:22
par Cercle » 08 Nov 2012, 19:22
Je pense avoir trouvé :
[(4(x+2)]-9(3-2x)] [4(x+2)+9(3-2x)]
((4x+8)-(27-18x)] [(4x+8)+(27-18x)]
[4x+8-27+18x] [4x+8+27-18x]
[22x-19][-14x+35]
(22x-19) (-14x+35)
C'est juste ? (j'espère..)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 19:26
par Carpate » 08 Nov 2012, 19:26
Cercle a écrit:Je pense avoir trouvé :
[(4(x+2)]-9(3-2x)] [4(x+2)+9(3-2x)]
((4x+8)-(27-18x)] [(4x+8)+(27-18x)]
[4x+8-27+18x] [4x+8+27-18x]
[22x-19][-14x+35]
(22x-19) (-14x+35)
C'est juste ? (j'espère..)
Tu as enfin repéré et utilisé l'identité remarquable !
Mais tu t'es trompé :
^2)
,
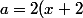)
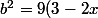^2)
,
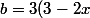)
Tu as encore besoin d'entraînement ...
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 19:59
par Cercle » 08 Nov 2012, 19:59
Et comme ça :
[(2(x+2)]-3[(3-2x)] [2(x+2)+3(3-2x)]
[(2x+4)-9+6x] [(2x+4)+9-6x]
[2x+4-9+6x] [2x+4+9-6x]
(8x-5) (-4x+13)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 20:33
par Carpate » 08 Nov 2012, 20:33
Cercle a écrit:Et comme ça :
[(2(x+2)]-3[(3-2x)] [2(x+2)+3(3-2x)]
[(2x+4)-9+6x] [(2x+4)+9-6x]
[2x+4-9+6x] [2x+4+9-6x]
(8x-5) (-4x+13)
Ouais, donc S= { ... ; ...}
-
Cercle
- Membre Naturel
- Messages: 28
- Enregistré le: 07 Nov 2012, 17:31
-
 par Cercle » 08 Nov 2012, 20:34
par Cercle » 08 Nov 2012, 20:34
Donc S= {-8;4}
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 08 Nov 2012, 20:48
par bentaarito » 08 Nov 2012, 20:48
Faux....!!
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Nov 2012, 21:02
par Carpate » 08 Nov 2012, 21:02
Cercle a écrit:Donc S= {-8;4}
Comme te l'a dit Bentaarito, ce n'est pas encore ça !!!
Si on détaille tout :



Fais de même pour

Et, encore une fois fais des exercices de calcul simple ...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 09 Nov 2012, 01:06
par Sylviel » 09 Nov 2012, 01:06
par ailleurs ouvrir un nouveau fil sur un sujet déjà largement débattu ça ne se fait pas vraiment...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
