Dm de 2nd sur géométrie analytique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kannelle
- Membre Naturel
- Messages: 27
- Enregistré le: 05 Nov 2012, 10:03
-
 par Kannelle » 05 Nov 2012, 18:24
par Kannelle » 05 Nov 2012, 18:24
Kikoo <3 Bieber a écrit:Quelle est l'opération que tu as faite pour trouver x=2/3 ?
Parce que d'un, c'est faux, et puis il me semble que tu appliques sans comprendre.
Explique-moi avec des mots ce que tu as fait.
mais la on a pas besoin de 2x=3!!!
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 05 Nov 2012, 18:32
par Kikoo <3 Bieber » 05 Nov 2012, 18:32
Kannelle a écrit:2x=2*x comme j'isole x je passe 2 de l'autre coté donc sont signe change et devien une division donc x=3/2
L'explication est confuse mais le résultat est là.
Lorsque l'on dispose de l'égalité suivante : a*b=c
Nous divisons des deux côtés par b (si et seulement si b est non nul !) pour isoler a.
On a alors : a=c/b
Tu n'as qu'à faire ceci pour trouver cos(ABC), il n'y a rien de difficile.
-
Kannelle
- Membre Naturel
- Messages: 27
- Enregistré le: 05 Nov 2012, 10:03
-
 par Kannelle » 06 Nov 2012, 11:31
par Kannelle » 06 Nov 2012, 11:31
AC²=AB²+BC²-2*AB*bc*cos(ABC)
320=89+233-2*89*233 *cos(ABC)
320-89-233=-289*233 *cos(ABC)
-2=-220737 *cos(ABC)
-2+41474=cos(ABC)
cos(ABC)=41472
Est-ce correct??
-
Kannelle
- Membre Naturel
- Messages: 27
- Enregistré le: 05 Nov 2012, 10:03
-
 par Kannelle » 08 Nov 2012, 14:22
par Kannelle » 08 Nov 2012, 14:22
Kikoo <3 Bieber a écrit:L'explication est confuse mais le résultat est là.
Lorsque l'on dispose de l'égalité suivante : a*b=c
Nous divisons des deux côtés par b (si et seulement si b est non nul !) pour isoler a.
On a alors : a=c/b
Tu n'as qu'à faire ceci pour trouver cos(ABC), il n'y a rien de difficile.
Est-ce correct???
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 08 Nov 2012, 14:29
par Kikoo <3 Bieber » 08 Nov 2012, 14:29
Voilà ce que tu dois faire pour trouver cos(ABC) en fonction des autres longueurs.
Il va falloir travailler les calculs !
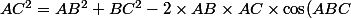\\<br />AC^2-AB^2-BC^2=-2\times AB\times AC\times \cos(ABC)\\<br />\cos(ABC)=\frac{AB^2+BC^2-AC^2}{2\times AB\times AC})
-
Kannelle
- Membre Naturel
- Messages: 27
- Enregistré le: 05 Nov 2012, 10:03
-
 par Kannelle » 08 Nov 2012, 18:42
par Kannelle » 08 Nov 2012, 18:42
Kikoo <3 Bieber a écrit:Voilà ce que tu dois faire pour trouver cos(ABC) en fonction des autres longueurs.
Il va falloir travailler les calculs !
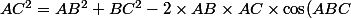\\<br />AC^2-AB^2-BC^2=-2\times AB\times AC\times \cos(ABC)\\<br />\cos(ABC)=\frac{AB^2+BC^2-AC^2}{2\times AB\times AC})
ok merci mais je bloque pour la b
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités