Limite d'une fonction ln en +oo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 13:04
par ThekamikazeFou » 06 Nov 2012, 13:04
bonjour,
pouvez vous m'expliquer comment calculer cette limite en +oo ?
f(x) = xln |
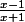
|
j'ai essayer en développement mais je ne vois pas comment trouver -2
merci
-
Freyja
- Membre Naturel
- Messages: 23
- Enregistré le: 05 Juil 2012, 07:34
-
 par Freyja » 06 Nov 2012, 13:43
par Freyja » 06 Nov 2012, 13:43
Quand peux-tu dire que la fonction Ln est à valeurs positives ?
Débute par une étude de signe de ta fonction f par intervalles.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 13:48
par ThekamikazeFou » 06 Nov 2012, 13:48
désolé j'ai changer le topic et poser une autre question, j'avais réussi à répondre à ma précédente question...
je sais désormais qu f(x) est décroissante de ]0,1[ puis croissante de ]1,+oo[
en
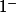
et
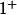
f(x) tend vers -oo
maintenant je cherche un moyen de trouver la limite en +oo

-
Freyja
- Membre Naturel
- Messages: 23
- Enregistré le: 05 Juil 2012, 07:34
-
 par Freyja » 06 Nov 2012, 14:08
par Freyja » 06 Nov 2012, 14:08
Commence à rétablir l'énoncé manquant dans un souci de cohérence.
Et puis supprime le signe de valeur absolue inutile au voisinage de

.
Alors que vaut la limite de la fraction rationnelle ? Que vaut celle de sa
composée par Ln ? Puis du produit par x ? Quel terme prépondérant ici
impose sa limite restrictive (ou pas) à son ensemble ? Qu'en conclure ?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 14:50
par ThekamikazeFou » 06 Nov 2012, 14:50
il n'y a pas vraiment d'énoncée manquant,
grace à la dérivée et à la dérivée second j'en ai conclue que f(x) sur

est décroissantede ]0,1[ puis croissante de ]1,+oo[
avec
f(x) = xln |
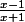
|
maintenant je cherche la limite en +oo
donc au voisinange de +oo
 = xln \frac{x-1}{x+1})
donc on à une limite de la forme

or
 = xln \frac{x-1}{x+1})
=
 = x( [ ln (x-1) - ln (x+1) ])

or
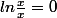
après je ne comprends pas vraiment ce que vous voulez que je fasse
-
Freyja
- Membre Naturel
- Messages: 23
- Enregistré le: 05 Juil 2012, 07:34
-
 par Freyja » 06 Nov 2012, 15:12
par Freyja » 06 Nov 2012, 15:12
Il s'agit de lever l'indétermination de Ln(h(x)) où h(x) est ta fraction, vers :

.
Or tu sais que :

et tu connais un DL de ln (1-x) au voisinage de 0.
Effectue donc un changement de variable approprié puis déduis-en la limite du tout.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 15:16
par ThekamikazeFou » 06 Nov 2012, 15:16
je vous l'ai dis justement ln(h(x)) tend vers 0 en +oo
mais apres jene vois pas comment faire la suite
-
Freyja
- Membre Naturel
- Messages: 23
- Enregistré le: 05 Juil 2012, 07:34
-
 par Freyja » 06 Nov 2012, 15:38
par Freyja » 06 Nov 2012, 15:38
ThekamikazeFou a écrit:je vous l'ai dis justement : ln(h(x)) tend vers 0 en +oo
mais après je ne vois pas comment faire la suite
Je l'ai écrit, aussi il faut prendre le temps d'analyser les réponses avant le flood.
Trouve ainsi un équivalent de cette fonction au voisinage de l'infini ([url="http://serge.mehl.free.fr/anx/dev_lim.html"]via les D.L[/url]).
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 15:41
par ThekamikazeFou » 06 Nov 2012, 15:41
Je ne flood pas, mais j'ai beau analyser je ne trouve pas, sachant que je n'ai jamais fais les développements limité et que je ne peux les utiliser...
je multipi ln(x-1) - ln (x+1) par son conjugué?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Nov 2012, 17:55
par chan79 » 06 Nov 2012, 17:55
ThekamikazeFou a écrit:Je ne flood pas, mais j'ai beau analyser je ne trouve pas, sachant que je n'ai jamais fais les développements limité et que je ne peux les utiliser...
je multipi ln(x-1) - ln (x+1) par son conjugué?
tu peux utiliser
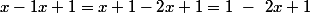
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 18:21
par ThekamikazeFou » 06 Nov 2012, 18:21
c'est ce que m'a proposer Freyja, mais je ne peux pas faire de développement limite.
enfait ce qui me pose problème c'est le x devant le Ln je ne comprend spas du tout comment on peut arrivé à un résultat négatif (-2)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Nov 2012, 18:46
par Carpate » 06 Nov 2012, 18:46
ThekamikazeFou a écrit:c'est ce que m'a proposer Freyja, mais je ne peux pas faire de développement limite.
enfait ce qui me pose problème c'est le x devant le Ln je ne comprend spas du tout comment on peut arrivé à un résultat négatif (-2)
 =x ln(\frac{x-1}{x+1}))
On pose
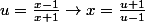
 = \frac{u+1}{u-1} ln(u))
Quand
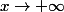
,

,

,
 \rightarrow 0)
,
 \rightarrow +\infty)
(because croissances comparées)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Nov 2012, 18:56
par Carpate » 06 Nov 2012, 18:56
Tu as raison !
je n'avais pas tracé la courbe !
Mais alors, sans D.L. comment le montrer ?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 19:32
par ThekamikazeFou » 06 Nov 2012, 19:32
Justement je ne sais pas...
Enfait c'est pas que je n'ai pas le droit mais on a jamais fais cela en cours.
Apres si je ne trouve vraiment pas je vais faire avec le D.L
Pouvez m'expliquer comment faire avec le D.L ? Ou du moin comment cela fonctionne?
-
Freyja
- Membre Naturel
- Messages: 23
- Enregistré le: 05 Juil 2012, 07:34
-
 par Freyja » 06 Nov 2012, 19:54
par Freyja » 06 Nov 2012, 19:54
ThekamikazeFou a écrit:Justement je ne sais pas...
Enfait c'est pas que je n'ai pas le droit mais on a jamais fais cela en cours.
Apres si je ne trouve vraiment pas je vais faire avec le D.L
Pouvez m'expliquer comment faire avec le D.L ? Ou du moin comment cela fonctionne?
Un D.L. de f n'est que l'approximation polynomiale de f au voisinage d'un point et s'exprime donc en un polynôme et un reste Rn d'ordre n négligeable quand la fonction devient suffisamment proche du point [url=http://fr.m.wikipedia.org/wiki/Développement_limité](voir wiki)[/url] et le
cours lycée.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Nov 2012, 20:24
par chan79 » 06 Nov 2012, 20:24
ThekamikazeFou a écrit:Justement je ne sais pas...
Enfait c'est pas que je n'ai pas le droit mais on a jamais fais cela en cours.
Apres si je ne trouve vraiment pas je vais faire avec le D.L
Pouvez m'expliquer comment faire avec le D.L ? Ou du moin comment cela fonctionne?
Tu pourrais essayer ça:
on pose X=(x-1)/(x+1)
quand x tend vers +inf, X tend vers 1
X=(x-1)/(x+1) donne x=(X+1)/(1-X)
il faut donc chercher la limite de
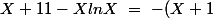. \fra{ln(X) - ln(1)}{X-1})
La dérivée de ln x étant 1/x, la fraction tend vers 1/1 et la limite est -(1+1)=-2
Attention à justifier toutes les étapes
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 06 Nov 2012, 21:16
par ThekamikazeFou » 06 Nov 2012, 21:16
Freyja, on ne fais pas les D.L au lycée.
Simple chan79
De plus pourquoi utilise tu la dérivé de lnx ?
Sinon merci beaucoup j'ai compris comme faire avec le taux de variation ! :)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Nov 2012, 08:09
par chan79 » 07 Nov 2012, 08:09
ThekamikazeFou a écrit:Freyja, on ne fais pas les D.L au lycée.
De plus pourquoi utilise tu la dérivé de lnx ?
Puisque tu ne connais pas les DL, il faut bien trouver une autre méthode
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 07 Nov 2012, 09:19
par Mathusalem » 07 Nov 2012, 09:19
Si on récrit

Il me semble que l'on a une forme indeterminée pour la limite que l'on peut lever avec la règle de bernoulli l'hospital.
On trouve en dérivant en haut en bas

Donc

Quand on prend la limite, ça tend vers -2.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités