ENSEMBLES (lycée)

[badrabdallaoui]

salut a tous :D
bon, j'ai rencontré une énorme difficulté à résoudre une partie d'un ex des ensembles.
ça serait gentil de votre part a m'aider de le résoudre(juste d'ou commecer ou la methode qu'il faut suivre ). la voici si dessous:

considérons les 3 ensembles E , E1 , et E2 définis par :
E1= {(x , x-(racine(x²-1))) , x >1 }
E2= {(x , x+(racine(x²-1))) , x >1 }
E = { (x,y);)R² / y²-2xy+1=0 et x>1 }

montrer que E = E1 U E2

bon je crois qu'il y aura plusieurs méthodes ,mais celle que je dois utilisé est celle de inclusion et inclusion réciproque.

Merci d'avance :))))

[Anonyme]

@badrabdallaoui

Piste de travail :
Si tu considères l'équation y²-2xy+1=0 comme une équation du second degré en y ( ay²+by+c=0 )
en calculant
Quelles sont les solutions de cette équation ?

ps)
oui tu as raison :
il faut démontrer que E est inclus dans E1 U E2 et que E1 U E2 est inclus dans E

[badrabdallaoui]

@badrabdallaoui

Piste de travail :
Si tu considères l'équation y²-2xy+1=0 comme une équation du second degré en y ( ay²+by+c=0 )
en calculant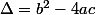
Quelles sont les solutions de cette équation ?

ps)
oui tu as raison :
il faut démontrer que E est inclus dans E1 U E2 et que E1 U E2 est inclus dans E

ah oui merci bcpp, je vois maintenant, mais il me parait que cette methode nous permette de montrer juste E inclus dans E1 U E2.

et quand on trouve que y=x+racine(x²-1) ou y=x-racine(x²-1) , peut-on directement poser l'équivalence suivante : y²-2xy+1=0 (x,x-(racine(x²-1)) ou (x,x+(racine(x²-1)) ?

[Anonyme]

@badrabdallaoui

Pourquoi ?

Conseil :
Ecris ce qu'est l'ensemble E : c'est l'ensemble des x tels que .....
et
Ecris ce qu'est l'ensemble E1 U E2 : c'est l'ensemble des x tels que .....

[badrabdallaoui]

et quand on trouve que y=x+racine(x²-1) ou y=x-racine(x²-1) , peut-on directement poser l'équivalence suivante : y²-2xy+1=0 <=>(x,x-(racine(x²-1)) ou (x,x+(racine(x²-1)) ?

[Anonyme]

@badrabdallaoui

D'après toi

Est ce qu'on a :

avec et les 2 solutions de l'équation

[badrabdallaoui]

Merci énormément :))

[Anonyme]

@badrabdallaoui
De rien
Cela a été un VRAI plaisir ! car tu poses des questions précises et on voit que tu as travaillé ton exercice...
Hélàs ce n'est pas le cas de beaucoup d'internautes qui postent des messages dans Maths-Forum uniquement pour obtenir des réponses toutes faites qui leur évitent de réfléchir ou de travailler les maths.... et c'est dommage pour eux....

A+