Devoir Maison : première
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 02 Nov 2012, 13:09
par FionaLucet » 02 Nov 2012, 13:09

Bonjour, voici le dm que j'ai à faire pour la rentrée. Je bloque à l'exercice 1, 2., d)
1. a) P9(x) = x²-(9-1)x+9+2 = x²-8x+11
Sachant que la forme canonique est de type :

On calcule

= -b/2a = 4
et

= -;)/4a = -5
c) P1(x) = x²-(1-1)x+1+2 = x²+3
2. a)

m = b²-4ac
= (m-1)² - 4(m+2)
= m² - 2m + 1- 4m - 8
= m² - 6m - 7
= m(m-6) -7

m = (m-7)(m+1)
= m² + m - 7m - 7
= m² - 6m - 7
= m(m-6) -7
b) (m-7)(m+1) = 0
soit (m-7) = 0
m = 7 = x1
soit (m+1) = 0
m = -1 = x2
P7(x) = (x - x0)² = (x - (-3))² = (x + 3)²
x0 = -b/2a = -6/2 = -3
P-1(x) = (x - x0)² = (x - 1)²
x0 = -b/2a = 1
c) Pm(x) n'est pas factorisable lorsque  m < 0
m < 0
(m - 7)(m + 1) < 0
soit m < 0 soit m < -1
Mais cela ne correspond pas car en réalité le trinôme n'est
pas factorisable quand m appartient à l'intervalle ]-1 ; 7[
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 02 Nov 2012, 13:22
par Arnaud-29-31 » 02 Nov 2012, 13:22
Bonjour,
Lorsque tu écris
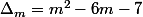
tu as un trinôme.
En montrant que -1 et 7 sont racine tu as immédiatement
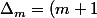.(m-7))
(C'est plus propre que de partir du résultat proposé et le développer pour montrer que c'est égal à l'expression de
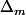
)
Ensuite pour la question d), ton trinôme
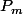
ne sera effectivement pas factorisable si

,
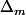
étant un trinôme, n'y a t'il pas une propriété qui donne le signe une fois que l'on a les racines ?
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 02 Nov 2012, 18:54
par FionaLucet » 02 Nov 2012, 18:54
Merci beaucoup .
C'est vrai que c'est plus propre par contre je n'ai pas très bien compris ...
(m+1)(m+7) c'est en fait la forme factorisée (x - x0)(x - x1) de ;)m ?
Ah oui ! Sachant que les racines sont -1 et 7 et que le trinôme est du signe
contraire de a c'est à dire ici négatif à l'intérieur des racines. Donc ;)m < 0
lorsque m appartient à l'intervalle ]-1 ; 7[ ?
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 04 Nov 2012, 11:54
par FionaLucet » 04 Nov 2012, 11:54
Merci beaucoup .
C'est vrai que c'est plus propre par contre je n'ai pas très bien compris ...
(m+1)(m+7) c'est en fait la forme factorisée (x - x0)(x - x1) de ;)m ?
Ah oui ! Sachant que les racines sont -1 et 7 et que le trinôme est du signe
contraire de a c'est à dire ici négatif à l'intérieur des racines. Donc ;)m < 0
lorsque m appartient à l'intervalle ]-1 ; 7[ ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Nov 2012, 12:04
par XENSECP » 04 Nov 2012, 12:04
What's up ? Tu en es où ?
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 04 Nov 2012, 18:10
par FionaLucet » 04 Nov 2012, 18:10
Toujours au même point ... je n'ai pas très bien compris :
(m+1)(m+7) c'est en fait la forme factorisée (x - x0)(x - x1) de ;)m ?
Mais cela suffit pour justifier que ;)m = (m-7)(m+1) ?
Ensuite pour le d) il s'agit donc bien de cette propriété et donc de
cet intervalle ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Nov 2012, 18:22
par XENSECP » 04 Nov 2012, 18:22
Tableau de signes en bref!?
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 04 Nov 2012, 18:52
par FionaLucet » 04 Nov 2012, 18:52
Oui mais pas obligé si j'énonce la propriété ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 04 Nov 2012, 18:56
par XENSECP » 04 Nov 2012, 18:56
Bah oui apprenons des trucs par coeur c'est amusant
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 04 Nov 2012, 20:46
par FionaLucet » 04 Nov 2012, 20:46
Un tableau de signes ne s'apprend pas contrairement à une propriété
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 05 Nov 2012, 16:06
par FionaLucet » 05 Nov 2012, 16:06
Pour le 3.a) je bloque à nouveau ...
On cherche quand -b-;);)/2a = 5
Ou quand -b+;);)/2a = 5
Donc je remplace b par (m-1) et

soit m²-6m-7 trouvé précedemment à la question 2.a)
Puis pour supprimer la racine j'élève tout au carré ce qui donne :

Le problème est que à la fin de mon développement je trouve : -2m² + 4m + 8 = 100
Je bloque car je ne sais plus comment faire et je ne sais pas si ce que j'ai fait est vraiment juste...
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 05 Nov 2012, 18:54
par XENSECP » 05 Nov 2012, 18:54
Ou tu peux être maligne et utiliser la forme "factorisée" pour trouver m ;)
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 06 Nov 2012, 11:33
par FionaLucet » 06 Nov 2012, 11:33
Merci j'ai trouvé ! sans utiliser la forme factorisée...
Pm(x) admet 2 racines x1 et x2 dont l'une d'entre elles vaut 5 donc x vaut 5.
On obtient alors Pm(5) = 5²-(m-1)5+m+2
;) 25-5m+5+m+2 = 0
;) 32-4m = 0
;) 32 = 4m
;) 8 = m
Donc si m vaut 8 alors Pm(x) admet une racine qui vaut 5.
Pour le 4. j'aimerais juste savoir si la rédaction est correcte :
On choisit P1(x) = x²+3
et P2(x) = x²-x+4
x²+3 = x²-x+4
3-4 = -x
1 = x
1 est donc l'abscisse du point I
P1(1) = 1²+3 = 4
4 est donc l'abscisse du point I
On vérifie alors que I appartient à la courbe de la fonction Pm(x)
Pm(1) = 1²-(m-1)1+m+2
= 1-m+1+m+2
= 4
Donc I appartient bien à la courbe de Pm(x) quelque soit m;)R
Ainsi toutes les courbes de la fonction Pm(x) passent bien par I.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 06 Nov 2012, 11:46
par XENSECP » 06 Nov 2012, 11:46
Oui bien vu. Je regarde la suite plus tard.
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 06 Nov 2012, 20:34
par FionaLucet » 06 Nov 2012, 20:34
Merci beaucoup !
Voilà pour l'exercice 2, par contre pour le 3. je ne sais pas si c'est juste :

-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 07 Nov 2012, 20:57
par FionaLucet » 07 Nov 2012, 20:57
Est ce que quelqu'un pourrais vérifier s'il vous plaît ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 07 Nov 2012, 21:02
par XENSECP » 07 Nov 2012, 21:02
Tu es tombée dans le panneau pour exo2 2) :)
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 08 Nov 2012, 10:41
par FionaLucet » 08 Nov 2012, 10:41
Pour le 2. en fait c'est l'inverse non ?
Si 1 < x< 4 alors -x²+5x-4 et inversement
ou à moins que ça reste toujours -x²+5x-4 ?
Je ne comprends pas très bien ...
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 08 Nov 2012, 20:04
par FionaLucet » 08 Nov 2012, 20:04
Pour le 2. en fait c'est l'inverse non ?
Si 1 < x< 4 alors -x²+5x-4 et inversement
ou à moins que ça reste toujours -x²+5x-4 ?
Je ne comprends pas très bien ...
et pour le 3. est que je suis sur la bonne piste
parce que je n'arrive toujours pas à avancer .
Merci !
-
FionaLucet
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Nov 2012, 11:39
-
 par FionaLucet » 09 Nov 2012, 10:54
par FionaLucet » 09 Nov 2012, 10:54
J'ai besoin d'aide merci ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités




