Bonsoir,
Alors je dois résoudre l'équation log5 X = logx 5, en appliquant une propriété pour changer la base j'arrive à log5 x = 1/logx 5 <=> (log5 x)^2 = 1 <=> log5 x = 1 <=> x = 5 donc voilà comme solution j'ai 5.
Cependant, dans mon cours les solutions indiquées sont 5 et 1/5, et je ne vois pas comment trouver le 1/5...
Merci d'avance :)
équation logaritme
10 messages
- Page 1 sur 1
Hello
En classe de Terminale on étudie essentiellement le logarithme Népérien fonction qui est notée Ln
Cette fonction Ln est souvent introduite aux élèves comme étant une des solutions de l'équation différentielle :
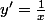 ( LA solution qui s'annule en 1 )
( LA solution qui s'annule en 1 )
Les fonctions Logarithmes ( à base avec
avec 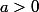 et qui est notée
et qui est notée  )
)
sont une famille de fonctions très simples "à mémoriser" et à "étudier" si on retient la formule :

=\frac{ln(x)}{ln(a)}) avec
avec 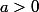 un nombre donné
un nombre donné
Remarque : La fonction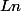 est la fonction logarithme à base
est la fonction logarithme à base  : on a
: on a 
=\frac{ln(x)}{ln(e)}=ln(x)) car
car =1)
Exemple : le log décimal
=\frac{ln(x)}{ln(10)})
Attention au signe de) : La fonction
: La fonction  définie par
définie par 
=log_{\frac{1}{2}}(x)) est une fonction décroissante sur
est une fonction décroissante sur 
En classe de Terminale on étudie essentiellement le logarithme Népérien fonction qui est notée Ln
Cette fonction Ln est souvent introduite aux élèves comme étant une des solutions de l'équation différentielle :
Les fonctions Logarithmes ( à base
sont une famille de fonctions très simples "à mémoriser" et à "étudier" si on retient la formule :
Remarque : La fonction
Exemple : le log décimal
Attention au signe de
Kikoo <3 Bieber a écrit:yop,
Tu dois traiter log5 x=logx 5 (je colle la base au log)
tu transformes selon la formule logb a=ln a / ln b
d'où : (ln(x))^2=(ln(5))^2
Or ln(1/5)=-ln(5) et je te laisse réfléchir...
Donc j'ai ln x/5 = ln 5/x
Je suis vraiment perdue... je vois pas d'où vient (ln(x))^2=(ln(5))^2 ni comment je peux résoudre mon calcul =s
vachounette01 a écrit:Alors, j'ai :
ln x / ln 5 = ln 5 / ln x (ln x)^2 = (ln 5)^2
comme ln 1/5 = -ln 5
(ln x)^2 = (-ln 1/5)^2 ?
Après je ne vois pas ce que je peux faire pour arriver à mes deux solutions
Ben non, t'y es presque !
Tu sais que ln a=ln b a=b
T'as quatre choix :
-ln x = ln 5
-ln x = -ln 5
ln x = ln 5
ln x = -ln 5
et tu verras que ceci se ramène à deux solutions possibles.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
