Matrice

[dilzydils]

Bonjour

j'ai un endomorphisme f de E=R3[X] qui à tout polynôme P associe: f(P)=(1+X^2)P"-2XP'.
J'arrive à montrer que la matrice de f dans la base (1, X, X^2-1, X+X^3/3) est diagonale avec 2 coefficients nuls et 2 autres qui valent -2.
Je dois montrer :
pour tt n dans N*, il existe h dans L(E) tel que h^n=f.

Pour n=1, h=f, à part ca, je passe aux matrices mais je m'en sors pas.

Merci

[flight]

salut

f(1)=0+0.x+0(x²-1)+0.(x+x^3/3)=0

f(x)=(1+x²).0-2x=-2x

f(x²-1)=(1+x²).2-4x²=2-2x²

f(x+x^3/3)=(1+x²)2x-2x(1+x²)=0

0 0 2 0
Mf= 0-2 0 0
0 0 2 0
0 0 0 0


à verifier...

[kms040584]

salut

f(1)=0+0.x+0(x²-1)+0.(x+x^3/3)=0

f(x)=(1+x²).0-2x=-2x

f(x²-1)=(1+x²).2-4x²=2-2x²

f(x+x^3/3)=(1+x²)2x-2x(1+x²)=0

0 0 2 0
Mf= 0-2 0 0
0 0 2 0
0 0 0 0


à verifier...

Salut,
non si tu ecris ta matrice dans la base considérée, ca donne bien la matrice diagonale donnée plus haut. Toi tu as écrit les images des vecteurs de base dans la base canonique... ca n'a pas vraiment de sens.

K.

[flight]

...oui exact big erreur de ma part !! desolé

[flight]

je me reprend :

f(1)=0
f(x)=-2x
f(x²-1)=-2(x²-1)
f(x-x^3/3)=0


Mf= 0 0 0 0
0 -2 0 0
0 0 -2 0
0 0 0 0

[nekros]

Salut,

Je crois que dilzydils avait déjà trouvé cette matrice...

Thomas G :zen:

[dilzydils]

Merci Nekros :++:

Je rappelle que la question est:

Je dois montrer :
pour tt n dans N*, il existe h dans L(E) tel que h^n=f.

Pour n=1, h=f, à part ca, je passe aux matrices mais je m'en sors pas.

Merci

[abcd22]

Bonsoir,
Le problème revient à trouver une racine nième de la matrice pour tout n. Si n est impair on peut prendre la matrice diagonale avec 0, racine nième de 2, racine nième de 2, 0 sur la diagonale.
Pour n pair (ça marche aussi pour n impair en fait), il suffirait de trouver une racine nième de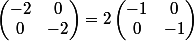 , il suffirait donc en fait de trouver une racine nième de , or à quelle transformation du plan (dont on peut trouver facilement une racine nième) correspond cette matrice ?

[dilzydils]

en dim2, ta matrice est celle de la symetrie centrale de centre O.
Une racine n-ieme serait une rotation d'angle Pi/n, mais comment ai-je le droit de passer de la matrice 4*4 à celle 2*2?

[abcd22]

On voit la matrice 4×4 comme une matrice diagonale par blocs, les blocs étant (0), , (0). Si on a une racine nième de chaque bloc on prend la matrice diagonale par blocs avec les racines nièmes et ça donne une racine nième de la matrice de départ. C'est possible qu'il y ait des racines nièmes de la matrice de départ qui ne soient pas de cette forme, mais on cherche juste une racine particulière ici.