Demonstrations!!!!!!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
capetien53
- Messages: 3
- Enregistré le: 01 Nov 2012, 22:26
-
 par capetien53 » 01 Nov 2012, 22:42
par capetien53 » 01 Nov 2012, 22:42
Bonjour a tous j'aimerais avoir vos reponses dans les plus bref delais. MERCI D'AVANCE
soit
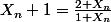
, X_1 superieure ou egale a 2.
Montrer que
a) X(1) > X(3) > X(5) > ...........
b) X(2) < X(4) < X(6) < ...........
Bon j'ai commence avec les sous-suites mais xa na rien donne
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 01 Nov 2012, 23:26
par Mortelune » 01 Nov 2012, 23:26
Bonsoir.
En posant
=\frac{2+x}{1+x})
on doit pouvoir montrer que f est décroissante et donc que
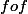
est croissante, ce qui donne une information sur la monotonie des sous-suites.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 01 Nov 2012, 23:27
par Arnaud-29-31 » 01 Nov 2012, 23:27
Bonsoir,
Ca ne donne rien d'extraire les deux sous suites adjacentes (

) et (
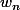
) telles que
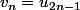
et
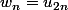
?
-
capetien53
- Messages: 3
- Enregistré le: 01 Nov 2012, 22:26
-
 par capetien53 » 02 Nov 2012, 04:32
par capetien53 » 02 Nov 2012, 04:32
soit un peu precis stp merci
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 02 Nov 2012, 11:17
par Mortelune » 02 Nov 2012, 11:17
Si on pose
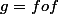
alors on peut définir les deux sous suites considérées dans l'énoncé à partir de

et

c'est à dire les suites
_n)
et
_n)
chacune des vérifiant
)
. Après il faut utiliser la propriété de croissance de g ...
-
Anonyme
 par Anonyme » 02 Nov 2012, 13:46
par Anonyme » 02 Nov 2012, 13:46
@capetien53
Le
1er "réflexe" à avoir quand on doit étudier une suite de ce type est d'expliquer :
pourquoi la suite
)
définie par la relation :
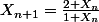
avec son 1ier terme
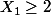
est une suite BIEN DEFINIE
C'est à dire :
expliquer pourquoi
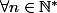
on a
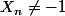
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités