Cherche équation

[Judoboy]

Ouais lâchez-le un peu ce pauvre Dzlogic. L'acharnement c'est mal, surtout quand ça vient d'un modérateur...Et je trouve que finalement à régler vos comptes avec lui dès qu'il post quelque part vous pourrissez bien plus les fils que lui...

[Anonyme]

@LeJeu

Je vais intrepréter ton message comme étant un compliment et non une blague ?
Cela me permettra de passer un bon week-end... enfin j'espère....

Comme on dit : l'espoir fait vivre

A+

[LeJeu]

@petitnoir
je confirme : passe un bon we !

[Kikoo <3 Bieber]

Faut pas être parano ptitnoir ^^

Ce que je vois derrière le message de lejeu, c'est de la franchise. Qu'il le dise si je me trompe. L'ironie c'est tout de même un peu plus visible...

[Anonyme]

@Kikoo <3 Bieber

y-a-pas de blem
essaie également de passer un bon we

[beagle]

excellent fil,
bonne discussion sur ce que j'en comprends.
La remarque de Sylvie me semble pertinente.

si l'énoncé semble ambigue , peut-ètre convient-il à chacun de dire pourquoi il fait ce qu'il répond.
Et donc à quel jeu il joue.C'est ce qu'a très bien recadré ptitnoir, il me semble.

sur l'habillage contesté par LeJeu,puis kikoo et judoboy difficile de juger du contextuel à l'ensemble du forum,
et Dlzlogic que j'aime bien par ailleurs devra porter cette croix sur l'ensemble des fils probabilistiques , du fait de son irrespect*..., alors...

*qui met en péril ses autres réponses de qualité

[Kikoo <3 Bieber]

Merci vous aussi ;) Pour ma part ce sera un long week-end de deux semaines pour faire le point sur ce que j'ai retenu de ce mois et demi à glander

[Judoboy]

Sinon ma réponse à la question initiale, même si ça a déjà été dit : on ne définit pas une fonction par sa valeur en 7 points. Tout ce qu'on peut dire d'une fonction qui vérifie les hypothèses de cet énoncé c'est qu'elle vérifie les hypothèses de l'énoncé. Une fonction qui vaut 4 en 1, 8 en 2 etc. elle peut valoir absolument n'importe quoi sur le reste de R.

[Anonyme]

@Kikoo <3 Bieber

D'après ton "travail"(activité) sur ce forum , je ne trouve pas que "tu as rien glandé"

Vive Toussaint et ses vacances !

[Kikoo <3 Bieber]

Merci !

J'ai peut-être été un forumeur prolifique (enfin c'est assez relatif aussi) mais en terme de travail personnel, ça n'a pas donné, et j'en ai payé les frais !
Il faut que je me recadre.

Fini le récit de ma vie, je te souhaite bon repos :)

[Anonyme]

@Kikoo <3 Bieber

Si tu ne te disperses pas trop , cela va payer...
Il faut BIEN SUR essayer de suivre en priorité tes objectifs !

Je pense que participer à un forum en répondant comme tu le fais à pleins de sujets de maths différents est forcément formateur , donc continue si tu peux !

[Kikoo <3 Bieber]

Tu as tout à fait raison, il faut que je vienne ici plus ponctuellement. Mais j'essaierai d'entretenir des échanges réguliers avec vous, les "habitués", vous m'apportez beaucoup ;)

PS : je crois que l'on va s'en arrêter là sinon ce sera considéré comme du polluage de topic ^^
Bonne nuit à tous, bonne nuit ptitnoir

[JlucBb]

Merci beaucoup de vos généreux efforts. Cela fait grand plaisir !

J'aurais du préciser : je suis dans une problématique de modélisation

Je complète mon énoncé :

valeurs de x : 1, 2, 3, 4, 5, 6, 7, 7,5, 8
valeurs de y : 4, 8, 12, 16, 22, 28, 38, 47, ?(valeur limite)

J'y vois logiquement l'addition d'une simple suite géométrique de raison 2 et d'une série 2, 2, 2, 2, 4, 4, 8, 16 où les valeurs doublent au-delà 4, puis en 6, puis en 7, puis en 7,5, puis je suppose en 7,75, 7,875 ... jusqu'à 8

J'ai un problème similaire pour les mêmes valeurs de x
valeurs de y : 15, 30, 45, 60, 85, 110, 155, 197,5, ?

[Anonyme]

@JlucBb
Est ce que pour modéliser ton système , une fonction définie par morceau (c'est à dire par intervalle) te convient ?
Par exemple :
si :
si : une autre expression telle que la fonction f soit continue en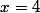

Et est ce que tu veux modéliser ton système UNIQUEMENT en utilisant des fonctions polynomiales en
c'est a dire du type

[Kikoo <3 Bieber]

Salut à vous,

Pour n'avoir rien posté d'utile hier soir, je rattrape mon retard :
Si le modèle est polynomial, on devra certainement passer par un polynôme de degré 7 (les valeurs ne suivent visiblement pas un schéma de proportionnalité).

soit z(x)=ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h

Un polynôme de degré 7 à coefficients réels. a est non nul.
On se propose de trouver ses coefficients a, b, c, d, e, f, g, h.

On pose donc un système de 7 équations à 7 inconnues qu'on résout comme on peut.

A partir de là je m'arrête car il se peut que cette méthode soit assez vaine devant plus d'astuce ;)

Sinon question : comment diagonalise-t-on la matrice associée ?

[Anonyme]

@Kikoo <3 Bieber

Je te conseille de lire ce document (pendant tes vacances , il fait 42 pages !)

Le but n'est pas de tout retenir mais de comprendre quelques notions et certaines méthodes
http://lpc2e.cnrs-orleans.fr/~ddwit/enseignement/cours_analnum.pdf

[fatal_error]

Bonjour JlucBb,

as-tu plus d'informations sur d'où proviennent tes nombres?
et deuxième question, as tu plus de données (pour les valeurs x=9, x=10 etc)
parce que les premières valeurs ont l'air "inutiles" (x=1..4), et c'est assez chaud avec uniquement de x=5 à 8.

[JlucBb]

Je suis dans la modélisation informatique des mathématiques pratiques à l'usage du joueur de billard (jeu par 3 bandes minimum). On se sert des repères disposés sur la grande bande (la découpant en 8 parties égales) et sur la petite bande (4 parties).

Pour l'instant, j'ai programmé en décomposant tous les segments (de 1 à 4, de 5 à 6, de 6 à 7; de 7 à 7,5). Mon but est bien évidemment la simplification et la généralisation via une ou deux formules.

[LeJeu]

Je suis dans la modélisation informatique des mathématiques pratiques à l'usage du joueur de billard (jeu par 3 bandes minimum). On se sert des repères disposés sur la grande bande (la découpant en 8 parties égales) et sur la petite bande (4 parties).

Pour l'instant, j'ai programmé en décomposant tous les segments (de 1 à 4, de 5 à 6, de 6 à 7; de 7 à 7,5). Mon but est bien évidemment la simplification et la généralisation via une ou deux formules.

On commence à entrevoir...Tu cherches la trajectoire de la boule suivant l'endroit ou elle rebondit sur la grande bande ?
t'aurais pas un dessin avec la position de la bille au départ ? et au final tu mesures quoi ?

[Dlzlogic]

Je complète mon énoncé :

valeurs de x : 1, 2, 3, 4, 5, 6, 7, 7,5, 8
valeurs de y : 4, 8, 12, 16, 22, 28, 38, 47, ?(valeur limite)

Code: Tout sélectionner

N° 1  x=1.00 y=4.00
N° 2  x=2.00 y=8.00
N° 3  x=3.00 y=12.00
N° 4  x=4.00 y=16.00
N° 5  x=5.00 y=22.00
N° 6  x=6.00 y=28.00
N° 7  x=7.00 y=38.00
N° 8  x=7.50 y=47.00
Régression polynôme Y=A.X^4 + B.X^3 + C.X^2 + D.X + E
  nbpts= 8  A = 0.04704  B = -0.6130  C = 2.95  D = -1.70  E = 3.43
Ecart-type (écart moyen quadratique) = 0.443
X=  8.00  ==> Y= 57.24
X=  8.50  ==> Y= 70.98
X=  8.75  ==> Y= 79.24
X=  9.00  ==> Y= 88.57


J'ai un problème similaire pour les mêmes valeurs de x
valeurs de y : 15, 30, 45, 60, 85, 110, 155, 197,5, ?

Code: Tout sélectionner

N° 1  x=1.00 y=15.00
N° 2  x=2.00 y=30.00
N° 3  x=3.00 y=45.00
N° 4  x=4.00 y=60.00
N° 5  x=5.00 y=85.00
N° 6  x=6.00 y=110.00
N° 7  x=7.00 y=155.00
N° 8  x=8.00 y=197.00
Régression polynôme Y=A.X^4 + B.X^3 + C.X^2 + D.X + E
  nbpts= 8  A = -0.07670  B = 1.681  C = -9.54  D = 34.2  E = -11.5
Ecart-type (écart moyen quadratique) = 1.917