Support

[zermel0]

Bonjour à tous, un bouquin affirme ceci :

Soit O relativement compact de U ouvert de R^n, soit P une Coo à support compact tel que supp P est dans O.

Pourquoi la distance de supp P à R^n\O est non nulle ?

[barbu23]

Bonsoir : :happy3:
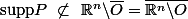
car est compact ( est en fait, relativement compact ), donc : , donc :happy3:
Parce que, par définition :

[zermel0]

Ok c'est clair, merci :)

[barbu23]

Regarde, j'ai corrigé, j'ai mis un peu d'ordre dans mes idées. :happy3:

[zermel0]

C'est nickel, merci. Je m'en sers dans la preuve du th de Meyers Serrin. Enfin moi je l'apprends la preuve hein.

C'était le dernier point manquant merciiii