Primitive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
dididu85
- Membre Naturel
- Messages: 42
- Enregistré le: 19 Fév 2010, 12:31
-
 par dididu85 » 25 Oct 2012, 21:03
par dididu85 » 25 Oct 2012, 21:03
Bonjour,
Je suis de nouveau en train de chercher une primitive. Mais je ne suis pas sur de mon résultat.
La fonction dont on cherche la primitive est la suivante :
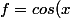^6*sin(x)^5)
Ma méthode est la suivante :
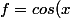^6*sin(x)*sin(x)^2*sin(x)^2)
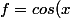^6*sin(x)*(1-cos(x)^2)*(1-cos(x)^2))
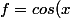^6*sin(x)-2*(sin(x)cos(x)^8)+(sin(x)cos(x)^10))
Est-ce que cela vous semble juste ?
Merci
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 25 Oct 2012, 21:14
par barbu23 » 25 Oct 2012, 21:14
Bonsoir, :happy3:
Il y'a plusieurs intégrations par parties à effectuer successivement :
Je te montre la première, et à toi de continuer le reste, mais c'est la même méthode.
 \sin^5 ( x ) dx = \int \sin ( x ) \cos^6 ( x ) \sin^4 (x) dx $)
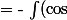' ( x ) \cos^6 (x) \sin^4 ( x ) dx = - \frac{1}{7} \cos^7 (x) \sin^4 ( x) + \frac{4}{7} \int \cos^8 (x) \sin^3 ( x ) dx + C $)
Continue à intégrer par partie, en diminuant l'exposant de
 $)
jusqu'à une plus petite valeur possible. Regarde comment tu avais au départ
 $)
, maintenant, tu as
 $)
, continue, à faire baisser la valeur de l'exposant de
 $)
Cordialement. :happy3:
-
dididu85
- Membre Naturel
- Messages: 42
- Enregistré le: 19 Fév 2010, 12:31
-
 par dididu85 » 25 Oct 2012, 21:21
par dididu85 » 25 Oct 2012, 21:21
C'est ce que j'ai réalisé en décomposant le sinus^6 en plusieurs sinus^2 puis en substituant cela à 1-cos^2.
Mon résultat final est de la forme
^7/7)+2(cos(x)^8/8)-(cos(x)^11/11))
Je pense que cela est correct mais je n'en suis pas certain
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 26 Oct 2012, 03:53
par fibonacci » 26 Oct 2012, 03:53
Bonjour;
^6 \sin (x)^5 dx = } \int {\cos (x)^6 \sin (x)^4 \sin (x)dx} \\ <br /> \\ <br /> {\rm{on pose}}\quad \left\{ \begin{array}{l}<br /> \cos (x) = t \\ <br /> dx = -\frac{{dt}}{{\sin (x)}} \\ <br /> \end{array} \right. \\ <br /> \\ <br /> \int {\cos (x)^6 \sin (x)^4 \sin (x)dx} = \int {t^6 (1 - t^2 )\sin (x)\frac{{-dt}}{{\sin (x)}}} \\ <br /> \\ <br /> \int {\cos (x)^6 \sin (x)^5 dx = }- \int {t^6 (1 - t^2 )^2dt} \\ <br /> \end{array})

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 26 Oct 2012, 07:58
par chan79 » 26 Oct 2012, 07:58
dididu85 a écrit:C'est ce que j'ai réalisé en décomposant le sinus^6 en plusieurs sinus^2 puis en substituant cela à 1-cos^2.
Mon résultat final est de la forme
^7/7)+2(cos(x)^8/8)-(cos(x)^11/11))
Je pense que cela est correct mais je n'en suis pas certain
salut
c'est plutôt

la méthode de fibonacci mène facilement au résultat
-
Black Jack
 par Black Jack » 26 Oct 2012, 12:32
par Black Jack » 26 Oct 2012, 12:32
sin^5(x) = sin^4(x).sin(x) = (1 - cos²(x))².sin(x) = (1 + cos^4(x) - 2cos²(x)).sin(x)
cos^6(x) * sin^5(x) = cos^6(x).(1 + cos^4(x) - 2cos²(x)).sin(x) = (cos^6(x) + cos^10(x) - 2cos^8(x)).sin(x)
S cos^6(x) * sin^5(x) dx = S cos^6(x).sin(x) dx + S cos^10(x).sin(x) dx - 2.S cos^8(x)).sin(x) dx
Et on a donc immédiatement, sans besoin d'aucun changement de variables. :
S cos^6(x) * sin^5(x) dx = - cos^7(x)/7 - cos^11(x)/11 + 2.cos^9(x)/9 + C
:zen:
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 26 Oct 2012, 13:03
par fibonacci » 26 Oct 2012, 13:03
C'est vrai ici parce que les exposants ne sont pas élevés
mais genre :
^{50} \sin (x)^{39} dx})
-
Black Jack
 par Black Jack » 26 Oct 2012, 13:24
par Black Jack » 26 Oct 2012, 13:24
fibonacci a écrit:C'est vrai ici parce que les exposants ne sont pas élevés
mais genre :
^{50} \sin (x)^{39} dx})
Cela ne change rien.
Le changement de variables n'empêchera nullement de devoir manipuler des puissances élevées.
La "difficulté" des calculs est la même.
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités