Puissance et factorielle

par **nekros** » 17 Juil 2006, 23:40

Salut,

Pour

et

, on note

l'exposant de la plus grande puissance de

divisant

.

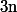
PS :

est l'ensemble des nombres premiers.

Montrer que

Bonne chance.

Thomas G :zen:

par **mln** » 18 Juil 2006, 01:33

Bonsoir,
On peut compter les multiples de chaque puissances de 2 <=1000 :

avec E la partie entière

par **nekros** » 18 Juil 2006, 01:49

Bien joué.
Si tu n'es pas fatigué, voilà la seconde partie :happy2:

Calculer

Bonne chance.

Thomas G :zen:

par **mln** » 18 Juil 2006, 01:51

j'aurais préféré :

parce qu'il n'y a pas de reste

par **mln** » 18 Juil 2006, 02:07

On peut faire la même chose que pour 2 et 1000!
alors Si pp^{b} [/tex]
Si

Si

avec E la partie entière.

On peut réunir toutes ces conditions dans une formule :

Voili voilou enfin Il me semble. Il est tard

On peut faire de même pour

avec

l'exposant de la plus grande puissance de d divisant m. Si d<=n, on a la même formule.

par **Mikou** » 18 Juil 2006, 10:43

salut nekros

On utilise la formule de legendre :

on a directement pour le resultat

par **nekros** » 18 Juil 2006, 12:28

Bonjour,

On pouvait aussi, pour simplifier les calculs, utiliser le fait que pour tout

dans

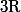
, on a :

Thomas G :zen:

par **aviateurpilot** » 18 Juil 2006, 19:28

je ne pense pa que c'est un exo olympiad