Equation complexe

[MrBrightside]

Bonsoir!

J'ai quelques soucis à faire un exercice sur les complexes, je fais donc appel à votre aide. Voici l'énoncé:

Montrer que a une racine imaginaire pure ib ; mettre (z-ib) en facteur et résoudre (E).
Que dire du triangle dont les sommets ont pour affixe les trois racines?



J'ai essayé de développer (E) puis de remplacer z par ib, mais ça ne me conduit à rien. Et je ne vois pas comment mettre (z-ib) en facteur. Des indications svp?

Merci.

[Pythales]

Bonsoir!

J'ai quelques soucis à faire un exercice sur les complexes, je fais donc appel à votre aide. Voici l'énoncé:

Montrer que a une racine imaginaire pure ib ; mettre (z-ib) en facteur et résoudre (E).
Que dire du triangle dont les sommets ont pour affixe les trois racines?



J'ai essayé de développer (E) puis de remplacer z par ib, mais ça ne me conduit à rien. Et je ne vois pas comment mettre (z-ib) en facteur. Des indications svp?

Merci.

Qu'est ce que ce 1+1 ?

[MrBrightside]

Une erreur de ma part, désolé! Il s'agit d'un (1+i), j'édite ça de suite.

[Pythales]

Une erreur de ma part, désolé! Il s'agit d'un (1+i), j'édite ça de suite.

Je m'en doutais.
Je ne comprends pas pourquoi tu n'aboutis pas en remplaçant par
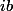
On obtient pour la partie réelle et pour la partie imaginaire.
A partir de là, c'est facile.

[MrBrightside]

Mmh, non vraiment je ne vois pas.

En plus je ne trouve pas les mêmes parties réelles et imaginaires que toi. Après mon calcul:

et

Et je ne vois pas en quoi ça m'avance en quoique ce soit... Les deux polynômes ont des racines que j'ai calculées, mais je ne vois absolument pas ce que ça m'apporte. :hum:

[MrBrightside]

Je retire ce que j'ai dit, mon calcul était faux, je viens de me rendre compte que j'ai oublié un exposant lorsque j'ai développé. Je dois le recommencer.

Edit: c'est bon, je trouve les mêmes parties réelles et imaginaires. Par contre je ne vois toujours pas en quoi ça m'avance. :we:

[Pythales]

Je retire ce que j'ai dit, mon calcul était faux, je viens de me rendre compte que j'ai oublié un exposant lorsque j'ai développé. Je dois le recommencer.

Edit: c'est bon, je trouve les mêmes parties réelles et imaginaires. Par contre je ne vois toujours pas en quoi ça m'avance. :we:

Il faut trouver une solution commune aux 2 équations.
Commence par le degré 2.

[MrBrightside]

C'est ce que j'ai fait, je trouve b=-2 ou b=5 dans l'éq de degré 2 et en remplaçant dans la deuxième, je trouve que -2 est également racine de l'éq de degré 3.

Mais je ne vois pas ce que je dois en déduire, et je ne vois pas à quoi me sert cette démarche.

[Pythales]

C'est ce que j'ai fait, je trouve b=-2 ou b=5 dans l'éq de degré 2 et en remplaçant dans la deuxième, je trouve que -2 est également racine de l'éq de degré 3.

Mais je ne vois pas ce que je dois en déduire, et je ne vois pas à quoi me sert cette démarche.

Ca veut dire que la racine que tu cherches est -

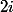
[MrBrightside]

Je m'en doutais un peu, mais je peux le déduire directement, simplement parce que -2 est une racine commune aux deux parties?


J'ai énormément de mal avec les complexes, donc des explications même les plus basiques sont les bienvenues. En tout cas merci de me consacrer du temps.

[Pythales]

Je m'en doutais un peu, mais je peux le déduire directement, simplement parce que -2 est une racine commune aux deux parties?


J'ai énormément de mal avec les complexes, donc des explications même les plus basiques sont les bienvenues. En tout cas merci de me consacrer du temps.

Si tu appelles ton polynôme, tu vois que car tu as montré que sa partie réelle et sa partie imaginaire sont nulles.
Je vais arréter là car j'ai eu une dure journée. Si ça peut t'aider, la réponse à la dernière question est : le triangle est isocèle rectangle.
Bonsoir

[Doraki]

Tu cherches un réel b tel que ib est racine de ton polynôme : tel que f(ib) = 0.
Tu calcules f(ib) et tu trouves f(ib) = b²-3b-10 + i(b3-2b²-3b+10).
Or il se trouve qu'un nombre complexe est nul quand sa partie réelle et sa partie imaginaire sont nuls.
Ici, comme b est réel, la partie réelle de f(ib) c'est le réel b²-3b-10 et la partie imaginaire de f(ib) c'est le réel b^3-2b²-3b+10.
Donc f(ib) est nul <=> ces deux quantités sont nulles.
(tu as traduit une égalité sur une quantité complexe en deux égalités sur des quantités réelles, qui sont plus faciles à aborder)

Comme tu as trouvé que -2 est la seule solution réelle du système b²-3b-10 = b^3-2b²-3b+10 = 0, ben tu sais donc que -2i est la seule racine imaginaire pure de ton polynôme.

[MrBrightside]

Merci pour ton aide Pythales, passe une bonne nuit.

Bonsoir Doraki, je comprends grosso modo, merci. Peux-tu m'aider pour la suite de l'exercice? Il faut que je mette (z-ib) en facteur, mais je ne vois absolument pas comment procéder... Et la question suivante aussi va me poser problèmes je le sens... :mur:

[Doraki]

Tu as déjà factorisé des polynômes ? genre si P(x) = x^3+x²+x-3 et que tu vois que 1 est racine, tu sais le factoriser par (x-1) ?

[MrBrightside]

Nope. Ça me rappelle vaguement un calcul indicatif d'un énoncé pour calculer une somme par télescopage mais c'est tout.

[Doraki]

Factoriser x^3+x²+x-3 par (x-1), comme son nom l'indique, c'est trouver les réels a,b,c tels que x^3+x²+x-3 = (x-1)(ax²+bx+c).
que vaut a ? que vaut b ? que vaut c ?

[MrBrightside]

a=1
b=2
c=3

Je vois comment faire, je vais m'occuper rapidement de cette factorisation puis j'irai me coucher car je commence à vraiment fatiguer...

Si tu peux m'apporter des éléments de réponse pour la suite, je regarderai ça demain matin, sinon c'est déjà gentil d'avoir été jusque là.

Je te souhaite une bonne nuit, à bientôt.

[Doraki]

Pour la suite faudra attendre que tu trouves explicitement les 3 racines.