F de signe constant

[nada-top]

we: hola everybody :++:
le probleme est le suivant: soit f une fonction continue sur un intervalle I telle que : pour tout x appartenant à I ; f(x)est différente de 0.
Démontrer que f a un signe constant. :++:

[hild]

Il suffit de raisonner par l'absurde. Tu suppose que sur ton intervalle, f n'est pas de signe constant. Il existe donc x1 tq f(x1)<0 et x2 tq f(x2)>0. Le théorème des valeurs intermédiaire, appliqué à f sur ]x1,x2[ permet de conclure qu'il existe au moins 1 x0 tq f(x0)=0 (car f est continue). Contradiction, d'où le résultat voulu.

[nekros]

Salut,

Par l'absurde :
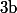
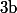
Supposons que pour tout , n'est pas de signe constant. Il existe donc a tel que et tel que avec et dans .

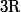
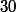
Donc il existe (évident) un tel que car est compris entre et
D'où la contradiction.
Donc si , alors est de signe constant.

Merci pour l'exo !

Thomas G :zen:

[nekros]

Arf, grillé par hild...
Trop lent en LATEX :triste:

Thomas G :zen:

[hild]

Désolé nekros...

Juste un commentaire : pour toi, le TVI est "évident"? C'est pourtant un théorème fondamental il me semble, bien qu'il soit intuitif...

D'accord, je chipote. :bad:

Merci en tout cas pour l'exo, nada-top!

[aviateurpilot]

c'est pas un exo olympiad
je l'ai vu l'année derniere au debut de l'année comme un exo d'activité .

[nekros]

Désolé nekros...

Juste un commentaire : pour toi, le TVI est "évident"? C'est pourtant un théorème fondamental il me semble, bien qu'il soit intuitif...

D'accord, je chipote. :bad:

Merci en tout cas pour l'exo, nada-top!

Graphiquement parlant, je pense que c'est évident.

Thomas G :zen: