Bonjour, je suis en seconde et je n'arrive pas à résoudre une équation car sur ma calculette je trouve
-1 mais pas sur ma copie.
Voilà mon équation et comment je l'ai faite:
(2x+5)² -2(7x+4) = 4(x+3)²-1
(2x+5)²-2(7x+4) = 4(x+2)(x+4)
4x²+20x+25-14x-8-4(x²+4x+2x+8)=0
4x²+6x+25-8-4x²-16x-8x-32=0
-18x-15=0
x=15/-18
Où est-ce que je me suis trompée svp ? (j'ai sauté qualques étapes).
Difficultés pour résoudre une équation
6 messages
- Page 1 sur 1
Bonjour,
Déjà, c'est une bonne démarche de vérifier son résultat. Le bon résultat est effectivement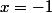 .
.
Ici, on ne peut pas factoriser : il faut donc développer. Il ne sert donc à rien d'écrire que^2-1=4(x+2)(x+4)) . En plus, c'est source d'erreurs, et dans ce cas c'est faux à cause du facteur 4 qui est en facteur de (x+3)^2 mais pas du -1. Le problème vient de cet endroit-là.
. En plus, c'est source d'erreurs, et dans ce cas c'est faux à cause du facteur 4 qui est en facteur de (x+3)^2 mais pas du -1. Le problème vient de cet endroit-là.
La version correcte est
et je te laisse continuer.
D'autre part, il est toujours plus efficace dans les calculs de regrouper les termes en x^2, les termes en x et les termes constants, et d'ordonner l'expression dans cet ordre.
Ainsi, on n'écrit pas+1=0) , mais on préfère écrire
, mais on préfère écrire 
Si tu veux en savoir plus, regarde la technique générale de résolution de ces équations en classe de seconde.
http://www.maths-forum.com/showthread.php?p=872393#post872393
Me00 a écrit:Bonjour, je suis en seconde et je n'arrive pas à résoudre une équation car sur ma calculette je trouve -1 mais pas sur ma copie.
Déjà, c'est une bonne démarche de vérifier son résultat. Le bon résultat est effectivement
Me00 a écrit:Voilà mon équation et comment je l'ai faite:
(2x+5)² -2(7x+4) = 4(x+3)²-1
Ici, on ne peut pas factoriser : il faut donc développer. Il ne sert donc à rien d'écrire que
La version correcte est
Me00 a écrit:4x²+20x+25-14x-8-4(x²+6x+9)+1=0
et je te laisse continuer.
D'autre part, il est toujours plus efficace dans les calculs de regrouper les termes en x^2, les termes en x et les termes constants, et d'ordonner l'expression dans cet ordre.
Ainsi, on n'écrit pas
Si tu veux en savoir plus, regarde la technique générale de résolution de ces équations en classe de seconde.
http://www.maths-forum.com/showthread.php?p=872393#post872393
Vérification d'Équations
Bonsoir, merci beaucoup de m'avoir aidée, pourriez vous (si ce n'est trop demander) vérifier mes résultats SVP ?
(x²-9)(2x+1)=(x+3)(2x+1)²
S= -1/2; -3; -4
4=(x racinecarréede 2 -1)²
S= 3 racinecarréede 2 / 2 ;-1 racinecarréede 2 /2
2x/x+1 = x+1 / 8x
S= 1/3; -1/5
2/x-1 = 1-x/x+1
S= -3
x²-x-3x/x+1 =0
S= 0; 2
Mais pour la dernière je ne suis pas sûre, je la trouve particulièrement dure.
Merci encore.
(x²-9)(2x+1)=(x+3)(2x+1)²
S= -1/2; -3; -4
4=(x racinecarréede 2 -1)²
S= 3 racinecarréede 2 / 2 ;-1 racinecarréede 2 /2
2x/x+1 = x+1 / 8x
S= 1/3; -1/5
2/x-1 = 1-x/x+1
S= -3
x²-x-3x/x+1 =0
S= 0; 2
Mais pour la dernière je ne suis pas sûre, je la trouve particulièrement dure.
Merci encore.
Me00 a écrit:Bonsoir, merci beaucoup de m'avoir aidée, pourriez vous (si ce n'est trop demander) vérifier mes résultats SVP ?
(x²-9)(2x+1)=(x+3)(2x+1)²
S= -1/2; -3; -4
OK
Me00 a écrit:4=(x racinecarréede 2 -1)²
S= 3 racinecarréede 2 / 2 ;-1 racinecarréede 2 /2
OK
Me00 a écrit:2x/x+1 = x+1 / 8x
S= 1/3; -1/5
OK (N'oublie pas d'écrire les parenthèse : c'est 2x/(x+1) = (x+1) / 8x, sinon ça veut dire 3=x+1/(8x), ce qui est différent).
Me00 a écrit:2/x-1 = 1-x/x+1
S= -3
Là il faut que tu écrives les parenthèses, parce que c'est ambigu.
Me00 a écrit:x²-x-3x/x+1 =0
S= 0; 2
Pareil, écris des parenthèses, parce que je ne sais pas si tu voulais dire
Me00 a écrit:Merci encore.
De rien.
Me00 a écrit:Merci beaucoup,
x² - x -(3x)/x+1 =0
je n'arrive pas à trouver le bon résultat. (je trouve 0 et 2).
Pouvez vous ma'aider dans la démarche qu'il faut suivre ?
Il faut aussi mettre des parenthèses au dénominateur!
C'est bien x^2 - x -(3x)/(x+1) =0 et non x^2 - x -(3x)/x+1 =0 qui s'écrirait x^2 - x -2 =0.
Ensuite, si tu multiplies tout par (x+1), on obtient (x+1)(x^2-x)-3x=0.
On peut factoriser par x. Alors, on obtient x[(x+1)(x-1)-3]=0, soit encore (identité remarquable)
x(x^2-4)=0, soit encore (identité remarquable) x(x-2)(x+2)=0.
Tes solutions étaient donc correctes, mais il manquait x=-2.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
