Primitive
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Juil 2006, 23:09
par Nightmare » 16 Juil 2006, 23:09
Sdec25 : celle-ci :
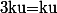
:happy3:
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:09
par Alexooo » 16 Juil 2006, 23:09
J'ai essayé d'appliqué précisement la formule qu'on m'a donné....^^
" Intégrale (a,b) f(x).dx = F(b) - F(a) "
Donc ici:
F(0) - F(R) or F(0) = 0
Et
F(R) = Intégrale de R² = R²x
D'ou ma réponse: - R²x...
ou me suis je trompé? dans le calcule de F(R) ? dans la formule?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:10
par Sdec25 » 16 Juil 2006, 23:10
Alexooo a écrit:Une derniere petite question pour la route

Je trouve -

Me suis-je totalement gourré?
Si on a une intégrale définie et que tu trouves un résultat qui dépend de x c'est que tu as fait une erreur.
Si c'est une primitive que tu as trouvé, dérive-là pour voir si tu retrouves la fonction de départ.
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:11
par Alexooo » 16 Juil 2006, 23:11
Sdec25 a écrit:Nightmare : de quelle propriété parles-tu ?
Alexooo : comment as-tu fais pour obtenir ce résultat ? On doit trouver du arctan dans la primitive.
hum, hum... du arc"quoi"? ^^
Jamais entendu parlé...

-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:12
par Sdec25 » 16 Juil 2006, 23:12
Alexooo ce n'est pas parce que f(0) = 0 que F(0) = 0.
et l'intégrale de a à b est F(b) - F(a) pas l'inverse.
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:13
par Sdec25 » 16 Juil 2006, 23:13
Alexooo a écrit:hum, hum... du arc"quoi"? ^^
Jamais entendu parlé...

La fonction réciproque de tangente :happy3:
dérivée de arctan = 1 / (1+x²)
Fait une division euclidienne de la fonction et une décomposition en éléments simples si nécessaire. Tu as déjà vu ça ?
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:13
par Alexooo » 16 Juil 2006, 23:13
Sdec25 a écrit:Si c'est une primitive que tu as trouvé, dérive-là pour voir si tu retrouves la fonction de départ.
lol suivant mon raisonement (a la noix) ça se tient...
Puisque dérivé de -R²x = -R² or -R² = - F(R) et -(F) = l'intégrale du départ... ^^
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:14
par Sdec25 » 16 Juil 2006, 23:14
Alexooo a écrit:lol suivant mon raisonement (a la noix) ça se tient...
Puisque dérivé de -R²x = -R² or -R² = - F(R) et -(F) = l'intégrale du départ... ^^
Si on dérive -R²x on obtient bien -R² mais on devrait trouver x² / (R² + x²), donc c'est pas bon.
Tu veux peut-être des explications sur les méthodes d'intégration ? :happy3:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 23:15
par nekros » 16 Juil 2006, 23:15
Comment as-tu procédé ?
Je propose un changement de variable.
Tu poses
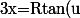)
et donc
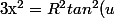)
D'autre part,
}du)
Donc
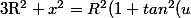)=\frac{1}{cos^2(u)})
Pour
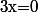
,
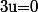
et pour
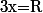
,

En remplaçant le tout, on a donc
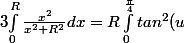du=[tan(u)-arctan(tan(u))]_0^{\frac{\pi}{4}}=1-\frac{\pi}{4})
Donc finalement,
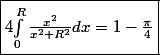
Thomas G :zen:
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:15
par Alexooo » 16 Juil 2006, 23:15
Sdec25 a écrit:Alexooo ce n'est pas parce que f(0) = 0 que F(0) = 0.
et l'intégrale de a à b est F(b) - F(a) pas l'inverse.
Lol effectivement j'étai un peu a l'ouest...^^
par contre le "sens" etait correct non? puisque c'est une intégrale de R a O, c'est bien F(O) - F(R) non?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:17
par Sdec25 » 16 Juil 2006, 23:17
Alexooo a écrit:Lol effectivement j'étai un peu a l'ouest...^^
par contre le "sens" etait correct non? puisque c'est une intégrale de R a O, c'est bien F(O) - F(R) non?
C'était pas de 0 à R ? enfin, pas d'importance si tu as compris :happy3:

et ça on sait intégrer.
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:20
par Alexooo » 16 Juil 2006, 23:20
Sdec25 a écrit:Tu veux peut-être des explications sur les méthodes d'intégration ? :happy3:
Oui ça serait pas de refus...
Et sinon, on est obligé de changé de variable?
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:22
par Alexooo » 16 Juil 2006, 23:22
Sdec25 a écrit:
et ça on sait intégrer.
Je sais que je suis embetant mais... pourquoi?
Tu trouve F(0) = 1 c'est ça?
Comment tu a fait?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:25
par Sdec25 » 16 Juil 2006, 23:25
Le changement de variable est parfois nécessaire, parfois non. Enfin commençons par le commencement :
Voici les 3 formules les + importantes.
 dx = F(b) - F(a))
 dx = k\int f(x) dx)
 + g(x) dx = \int f(x) dx + \int g(x) dx)
Tu n'as pas le droit de faire autre chose, comme l'intégrale d'un produit, ça ne marche pas !
Il faut toujours calculer la primitive même si une borne est 0.
Pour ton intégrale on peut faire avec ou sans CDV.
Moi j'ai mis la fonction sous une forme qu'on sait intégrer et c'est presque fini.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 23:26
par nekros » 16 Juil 2006, 23:26
Alexooo, regarde mon post 69, j'ai trouvé la réponse je l'espère...
Thomas G :zen:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:28
par Sdec25 » 16 Juil 2006, 23:28
Alexooo a écrit:Je sais que je suis embetant mais... pourquoi?
Tu trouve F(0) = 1 c'est ça?
Comment tu a fait?
Met tout au même dénominateur et tu trouveras la même chose :happy3:
Pour trouver ce résultat j'ai fait une division euclidienne (via un logiciel c'est plus pratique).
Pourquoi F(0)=1 ? Tant que tu n'as pas la primitive ne t'occupe pas de savoir ce que vaut F(0).
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:30
par Alexooo » 16 Juil 2006, 23:30
Sdec25 a écrit: dx = F(b) - F(a))
ha...
Je crois qu'il y a une erreur sur mon cahier...
Y'a marqué :
 dx = F(b) - F(a))
...
y'a une erreur?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 16 Juil 2006, 23:31
par Sdec25 » 16 Juil 2006, 23:31
oui c'est F(b) - F(a) pour l'intégrale de a à b et pas l'inverse, les 3 formules que je t'ai données sont les + importantes, à connaître absolument.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 16 Juil 2006, 23:32
par nekros » 16 Juil 2006, 23:32
effectivement...
Thomas G :zen:
-
Alexooo
- Membre Naturel
- Messages: 39
- Enregistré le: 16 Juil 2006, 16:32
-
 par Alexooo » 16 Juil 2006, 23:33
par Alexooo » 16 Juil 2006, 23:33
nekros a écrit:Alexooo, regarde mon post 69, j'ai trouvé la réponse je l'espère...
Thomas G :zen:
Merci
mais j'aimerais comprendre comment faire sans changement de variable car c'est quelque chose que je suis pas "sensé" avoir vu a ce niveau du livre.
(ceci dit, je suis sensé les avoir vu en terminal, ça m'empeche pas de pas reussir a les faire ^^)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités

 dx = F(b) - F(a))
 dx = k\int f(x) dx)
 + g(x) dx = \int f(x) dx + \int g(x) dx)
