Primitive

par **Alexooo** » 16 Juil 2006, 22:29

Nightmare a écrit:la fonction c'est f, et à tout nombre x elle associe le nombre f(x). Comprends-tu ?

Ok, j'ai compris :id:

par **nekros** » 16 Juil 2006, 22:31

Salut,

Pose

et donc

Pose

On a donc

Or,

, avec

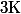
une constante réelle.

Finalement,

Donc

avec

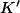
réel (

)

Thomas G :zen:

par **Nightmare** » 16 Juil 2006, 22:31

"uv' vaut x^n/n+1" :triste:
uv' est une fonction, x^n/n+1 un nombre :lol3: toujours la même histoire !

Bref, 1/(n+1) est une constante déjà, puisqu'on intégre par rapport à x, or les primitives du ku où k est réel et u est une fonction sont les fonctions kU où U est une primitive de u (modulo constante)

Donc il te suffit de primitiver x->x^n et de multiplier le résultat par 1/(n+1) et tu as tes primitives de x->x^n/(n+1)

:happy3:

par **Alexooo** » 16 Juil 2006, 22:32

Sdec25 a écrit:Pour x^n. ln x on peut faire une IPP pour trouver l'intégrale I(n) en fonction de l'intégrale I(n-1) de x^(n-1). ln x, et par une relation de récurrence on doit pouvoir trouver l'intégrale I(n).

lol
Je t'avou que je suis completement rouillé, je suis meme pas sur qu'en terminal (a l'époque ou j'etais sensé faire des maths ^^) je savais faire ça... donc maintenant apres 3 ans, la "récurrence" ça veut plus dire grand chose pour moi ^^

En fait je cherche vraiment a aller au plus simple, en théorie les exercices que je fais doivent pouvoir etre fait en moins de 1 min (donc il faut vraiment pas se compliquer)

par **Sdec25** » 16 Juil 2006, 22:33

Nightmare a écrit:Oui, ça c'est pour les physicien c'est bien ce que je dis :lol3:

Les physiciens utilisent cette notation pour être précis mais les matheux l'utilisent aussi (par exemple pour calculer la dérivée des fonctions réciproques).
D'ailleurs on devrait toujours utiliser cette notation mais c'est vrai qu'on l'utilise jamais (pour utiliser moins d'encre peut-être :ptdr: ).

par **Nightmare** » 16 Juil 2006, 22:36

Je n'ai jamais dit qu'on utilisait pas cette notation, j'ai dit qu'on l'interpretait mal :happy3:

Sinon pour revenir à l'intégrale, je suppose que n est un entier naturel mais si jamais il décrit Z tout entier, il faut faire attention au cas où n=-1

:happy3:

par **Sdec25** » 16 Juil 2006, 22:37

Alexooo a écrit:lol
Je t'avou que je suis completement rouillé, je suis meme pas sur qu'en terminal (a l'époque ou j'etais sensé faire des maths ^^) je savais faire ça... donc maintenant apres 3 ans, la "récurrence" ça veut plus dire grand chose pour moi ^^

En fait je cherche vraiment a aller au plus simple, en théorie les exercices que je fais doivent pouvoir etre fait en moins de 1 min (donc il faut vraiment pas se compliquer)

En fait pas besoin de récurrence ici (nekros a calculé la primitive) puisque en dérivant ln on obtient 1/x, j'ai confondu avec les intégrales comportant des exp.

Récurrence veut simplement dire qu'on obtient I(n) en fonction de I(n-1), ou l'inverse. Donc si on connaît I(0) on peut connaître I(n).

par **Alexooo** » 16 Juil 2006, 22:38

nekros a écrit:

Thomas G :zen:

C'est la que je comprend pas: on a le droit de "sortir" 1/n+1 comme ça?

par **nekros** » 16 Juil 2006, 22:41

Oui à mon avis

...

Sinon Alexooo, as-tu compris le calcul ?

Thomas G :zen:

par **Nightmare** » 16 Juil 2006, 22:41

Alexooo a écrit:C'est la que je comprend pas: on a le droit de "sortir" 1/n+1 comme ça?

J'ai donné l'explication plus haut, il s'agirait de lire ce que j'écris :lol3:

par **Sdec25** » 16 Juil 2006, 22:41

Nightmare a écrit:Je n'ai jamais dit qu'on utilisait pas cette notation, j'ai dit qu'on l'interpretait mal :happy3:

Sinon pour revenir à l'intégrale, je suppose que n est un entier naturel mais si jamais il décrit Z tout entier, il faut faire attention au cas où n=-1

:happy3:

Je comprend ce que tu veux dire, c'est vrai qu'on l'utilise pas souvent, mais je voulais juste dire que c'était plus "normal" de l'utiliser (au moins on comprend ce qu'on fait) :we:
Après, c'est vrai les matheux simplifient au maximum et on utilise des f' parce que dériver 50 fois en utilisant d/d c'est pas très pratique :happy3:

par **nekros** » 16 Juil 2006, 22:44

Par Nightmare : "Bref, 1/(n+1) est une constante déjà, puisqu'on intégre par rapport à x"

Thomas G :zen:

par **Nightmare** » 16 Juil 2006, 22:45

Bah on peut toujours utiliser

:happy3:

par **Alexooo** » 16 Juil 2006, 22:46

Nightmare a écrit:1/(n+1) est une constante déjà, puisqu'on intégre par rapport à x, or les primitives du ku où k est réel et u est une fonction sont les fonctions kU où U est une primitive de u (modulo constante)

Donc il te suffit de primitiver x->x^n et de multiplier le résultat par 1/(n+1) et tu as tes primitives de x->x^n/(n+1)

:happy3:

Oui j'avais lu desolé, mais je ne le savais pas...

C'est une regle générale ? que primitive de ku est kU si k est réel (avec U primitive de u)?

par **Nightmare** » 16 Juil 2006, 22:46

Bien sûr mais la question est sais-tu d'où elle vient ? La réponse sera simple si tu as bien compris la notion de primitive, plus difficile sinon :lol3:

par **Sdec25** » 16 Juil 2006, 22:50

Alexooo a écrit:Oui j'avais lu desolé, mais je ne le savais pas...

C'est une regle générale ? que primitive de ku est kU si k est réel (avec U primitive de u)?

Oui on en a déjà parlé au début du topic, c'est la propriété de linéarité :
intégrale de a + b = int de a + int de b
intégrale de k.a = k.int de a

par **Alexooo** » 16 Juil 2006, 22:58

Une derniere petite question pour la route

Je trouve -

Me suis-je totalement gourré?

par **Nightmare** » 16 Juil 2006, 22:59

Hum ... Je reste sceptique, la propriété de linéarité de l'intégrale et celle qui nous interresse sont proches mais aucune des deux n'explique l'autre.

par **Nightmare** » 16 Juil 2006, 23:01

Alexooo a écrit:Une derniere petite question pour la route

Je trouve -

Me suis-je totalement gourré?

Hum oui,ce n'est pas juste, comment as-tu trouvé ça ?

par **Sdec25** » 16 Juil 2006, 23:06

Nightmare : de quelle propriété parles-tu ?
Alexooo : comment as-tu fais pour obtenir ce résultat ? On doit trouver du arctan dans la primitive.

Primitive

Qui est en ligne