Petite question de probabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 09 Oct 2012, 15:16
par Ouimet21 » 09 Oct 2012, 15:16
Bonjour,
Soit
)
indépendantes;
Notons
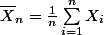
;
Notons
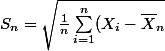^2})
;
1re question: Pour un

fixe, est-ce que les

sont indépendants?
Maintenant, notons

est fixe.
2e question: Pour un

fixe, est-ce que les

sont indépendants? Autrement dit, est-ce que les

conditionnellement à

sont indépendants?
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 10 Oct 2012, 18:02
par DamX » 10 Oct 2012, 18:02
Bonjour,
Intuitivement je dirais que non les variables "rescalées" par leur variance empirique ne sont pas indépendantes. Hélas je n'ai pas de preuve matérielle à t'apporter pour le moment.
Mais pour t'expliquer un peu mon intuition (on ne sait jamai quelqu'un d'autre rebondira peut être dessus ou ça te donnera des idées), si tu prend n=2, et dans le cas simplifé mu=0. tu as en fait Y1 = X1/|X1-X2| et Y2 = X2/|X1-X2|, et la question porte sur l'indépendance entre Y1 et Y2.
si tu prends un L très grand, la proba que Y1>L ne sera pas si petite que Ca Grace aux cas où X1 et X2 sont proches rendant l'etat Y1 très grand plausible. Meme raisonnement pour Y2<-L (dans le cas ou X1 et X2 sont tous les deux très négatifs cela rend plausible l'événement).
A présent si tu considères l'événement (Y1>L et Y2<-L), il est vraiment très improbable Parce qu'on ne peut pas vraiment avoir X1 et X2 très proches et de signes différents .. Pour cela je doute que P(Y1>L et Y2<-L) soit égal à P(Y1>L)P(Y2<-L) et donc au fait que Y1 et Y2 soient indépendants.
Je ne sais pas si mes explication font beaucoup de sens, j'essaierai plus tard de poser tout Ca en quelque chose de concret. (et d'ailleurs je me trompe peut-être)
Damien
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 10 Oct 2012, 18:12
par DamX » 10 Oct 2012, 18:12
Ah ben en fait c'est tout bête,
Si X1 et X2 sont de signe opposé on a alors forcement |Y1|<1 et |Y2|<1,
donc en fait P(Y1>1 et Y2<0) = 0 alors que P(Y1>1)P(Y2<0)>0.
D'où la non-indépendance.
Et je suppose qu'en creusant un peu on doit pouvoir trouver un critère similaire dans le cas n>2
Damien
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 10 Oct 2012, 18:49
par DamX » 10 Oct 2012, 18:49
Et en effet ça se généralise bien :
Dans le cas général n,
Si tu te places dans les cas X1>0 et X2<0,...,Xn<0, tu peux voir que dans ce cas Sn>X1/racine(n).
Et du coup Y1 = X1/Sn < racine(n)
De fait l'événement (Y1>racine(n), Y2<0,...,Yn<0) est de probabilité nulle alors que le produit des probas P(Y1>racine(n))P(Y2<0)...P(Yn<0) est > 0. D'où la non-indépendance.
Il y a peut etre des moyens beaucoup plus simples de le montrer, je ne sais pas :)
Damien
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités