Intégrale avec 2 paramètres

[besten]

Bonsoir,

On nous propose de discuter, suivant les valeurs des paramètres et la nature de l'intégrale .

Puis on doit calculer l'intégrale lorsqu'elle est convergente.

Comment on doit s'y prendre ?

[Alannaria]

Pose : . Où est-elle définie et continue ?
Pour quels et , existe-t-elle et converge-t-elle ?

[besten]

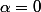
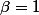
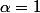
est convergente quand et ou et .

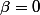
Je ne vois pas trop où tu veux en venir.

[lartdeladivisionparzero]

Pas seulement. Ne serait-ce qu'en se fiant au critère de Riemann, il y a bien plus de valeurs de a et b pour lesquelles l'intégrale est convergente

[besten]

Pas seulement. Ne serait-ce qu'en se fiant au critère de Riemann, il y a bien plus de valeurs de a et b pour lesquelles l'intégrale est convergente

Comment on détermine ces valeurs ?

[lartdeladivisionparzero]

Alors j'utiliserai personnellement le critère de Riemann.
Je précise, j'ai pas mal de progrès à faire côté intégration et il est tard donc j'espère ne pas dire n'importe quoi mais on n'est jamais sûr de rien ...
Alors déjà le dénominateur est égal à t^b + t^a t^b
Je te conseille de séparer les cas déjà où b>1 et b;)1 (un cas se fait immédiatement, l'autre il faut un peu raisonner et trouver ensuite une condition aussi sur a)

[barbu23]

Bonsoir, :happy3:
Il faut appliquer la proposition suivante :
Si à l'infini et est de signe constant, alors et sont de même nature. :happy3:
Donc, il faut chercher un équivalent à l'infini de l'integrande.
Je vous laisse continuer. :happy3:

[besten]

Il faut appliquer la proposition suivante :
Si à l'infini et est de signe constant, alors et sont de même nature.
Donc, il faut chercher un équivalent à l'infini de l'integrande.

Je ne vois pas où tu veux en venir, je préfère la solution précédente mais si c'est mieux, j'aimerais comprendre ta méthode.

[barbu23]

Par exemple : à l'infini, sous certaines conditions appliquées sur et , donc : et sont de même nature. Et, il me semble que tu connais, les integrales de Riemann : ... Elles convergent ou elles divergent ?

[besten]

elles convergent si et sont supérieurs à 0

[barbu23]

elles convergent !

Il y'a certaines valeurs de et pour lesquelles elles convergent, comme il y'a certaines valeurs de \alpha et où elles divergent. Tu trouveras ça dans ton cours si tu y jettes un œil.

[barbu23]

elles convergent si et sont supérieurs à 0

Tu termines le travail seul alors, puisque tu arrives à comprendre le principe. :lol3:
Elles convergent si ... etc
Regarde dans ton cours en même temps.

[besten]

Merci du coup de main
Je ferai ça demain matin, si je n'y arrive pas, je sais où je peux avoir de l'aide :lol3:
bonne nuit :dodo: