Problème d'encadrement

[Cephal]

Bonjour à tous,
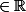
pour tout x , on considère la série de terme général converge, n .

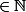
On a: .
On sait que la série converge normalement.
Il faut montrer que:


J'ai réussi à montrer: mais après je suis bloqué et je ne sais pas si je suis parti dans la bonne direction. Si vous avez des idées pour arriver à l'inégalité du dessus, je suis preneur.
Merci d'avance pour vos réponses.

[lartdeladivisionparzero]

C'est une majoration grossière qu'il te suffit de faire.
Pars de 2[sinx^2]/(exp(nx)+exp(-nx) (edit les crochets sont les valeurs absolues)
Ensuite tu as sinx^2 ;) x^2 que tu peux sortir de la somme vu qu'il ne dépend pas de l'indice. Ensuite j'ai remarqué que exp(-nx) est toujours positif donc je majore le tout par 2x^2/exp(nx)
Il te suffit de remarquer quelque chose sur cette suite pour calculer la somme de la série. et tu as la majoration voulue

[Cephal]

Encore merci pour ta réponse lartdeladivisionparzero, bonne soirée!

[lartdeladivisionparzero]

Toujours un plaisir, d'autant que je me refais les sujets de séries en ce moment :)
Bonne nuit à toi !

[Cephal]

j'ai un autre petit problème pour montrer la convergence d'une série et donc pour calculer la somme, je ne sais pas comment faire, sachant qu'au préalable, il fallait démontrer la règle de de Raabe-Duhamel, c'est-à-dire:
SI ALORS avec C>0. De plus la série de terme converge.
Merci d'avance pour votre aide.