Espaces Vectoriels.
5 messages
- Page 1 sur 1
Espaces Vectoriels.
Bonjour, je suis en L2 Phyique, et je revois une fois encore les bases de l'algèbre linéaire, que disons je maitrise en tant que leçon abstraite, mais où je peine à apercevoir le sens concret de certains termes. J'ai compris que la dimension d'un ensemble vectoriel est le nombre de vecteurs non colinéaires entre eux qu'il contient ... Mais je ne comprends pas le sens d'une base ou du rang en termes triviaux ... Merci d'avance à ceux qui auront la patience de me répondre !
Aberline a écrit:Bonjour, je suis en L2 Phyique, et je revois une fois encore les bases de l'algèbre linéaire, que disons je maitrise en tant que leçon abstraite, mais où je peine à apercevoir le sens concret de certains termes. J'ai compris que la dimension d'un ensemble vectoriel est le nombre de vecteurs non colinéaires entre eux qu'il contient ... Mais je ne comprends pas le sens d'une base ou du rang en termes triviaux ... Merci d'avance à ceux qui auront la patience de me répondre !
Pas exactement, la définition de la dimension que tu donnes est même fausse : il y a une infinité de vecteurs non colinéaires entre eux.
La dimension d'un espace vectoriel est une le cardinal d'une base de l'espace, ou plus concrètement le nombre minimal de vecteur qu'il te faut pour obtenir tous les autres par combinaison linéaire.
Pour mieux comprendre tu peux voir ça en terme de nombre de directions possible dans l'espace :
-> Sur une droite : 1 seule direction possible (la droite) soit dimension 1
-> Dans un plan : deux directions possibles (par exemple vers le nord ou vers l'est), et des combinaisons linéaires (nord est, nord ouest, sud ouest, etc...)
etc...
Ceci explique dimension et base.
Concernant le rang cela dépend du rang de quel objet tu parles
Salut
Autres explications :
Etant donné un espace vectoriel E
S'il existe des vecteurs de
de  tel que tout vecteur
tel que tout vecteur  de
de  s'écrit comme combinaison linéaire de
s'écrit comme combinaison linéaire de  , à savoir :
, à savoir :  où
où  sont des scalaires. on dit que la famille
sont des scalaires. on dit que la famille ) est une famille génératrice de
est une famille génératrice de  .
.
Si posséde une famille génératrice
posséde une famille génératrice ) tel que : si on enlève un seul vecteur à
tel que : si on enlève un seul vecteur à  elle n'est plus génératrice , on dit alors que
elle n'est plus génératrice , on dit alors que  est une base de
est une base de  et que
et que  est la dimension de
est la dimension de  .
.
Concrétement, une base de est une famille génératrice "avec juste ce qu'il faut " de vecteurs ( on dit famille génératrice minimale).
est une famille génératrice "avec juste ce qu'il faut " de vecteurs ( on dit famille génératrice minimale).
Dans ce cas lorsqu'un vecteur s'écrit : , il y'a unicité des scalaires
, il y'a unicité des scalaires  lesquels sont appelés les coordonnées de
lesquels sont appelés les coordonnées de  dans la base
dans la base  .
.
L'entier est bien entendu un invariant : si
est bien entendu un invariant : si ) et
et ) sont deux bases d'un même espace vectoriel
sont deux bases d'un même espace vectoriel  alors forcément
alors forcément 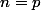 .
.
Autres explications :
Etant donné un espace vectoriel E
S'il existe des vecteurs
Si
Concrétement, une base de
Dans ce cas lorsqu'un vecteur s'écrit :
L'entier
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
